高二数学期末复习讲义（4）
直线与平面垂直
一．复习目标：
1．掌握直线与平面垂直的定义、判定定理和性质定理，并能运用它们进行论证和解决有关的问题；2．会用三垂线定理及其逆定理证明线线垂直，并会规范地写出解题过程。
二．知识要点：
1．直线与平面垂直的判定定理：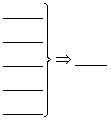
；性质定理：
；
三垂线定理：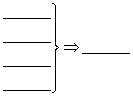
；三垂线定理的逆定理 : ；
2．证明直线和平面垂直的常用方法有：
3、目前所学过的证明线线垂直的方法有：（用符号表示）
（1）线垂直面：
（2）三垂线定理及逆定理：
（3）勾股定理的逆定理：
（4）异面直线夹角：
4、直线和平面所成角的范围：___________________ ；斜线呢？_________________
求斜线与平面所成角的方法有:
三．课前预习：
1．若
表示直线，
表示平面，下列条件中，能使
的是 （ ）
2．已知
与
是两条不同的直线，若直线
平面，①若直线
，则
；②若
，则
；③若
，则；④，则。上述判断正确的是
（ ）
①②③ ②③④ ①③④ ②④
3．在直四棱柱
中，当底面四边形
满足条件 时，
有
（注：填上你认为正确的一种条件即可，不必考虑所有可能的情况）
4.设三棱锥
的顶点
在平面
上的射影是
，给出以下命题：
①若
，
，则是
的垂心
②若
两两互相垂直，则是的垂心
③若
，是
的中点，则
④若，则是的外心
其中正确命题的命题是
四．例题分析：
例1．四面体中，
分别为
的中点，且
，
，求证：
平面
证明：
例2．如图是所在平面外一点，
平面
，
是
的中点，
是
上的点，
（1）求证：
；（2）当
，
时，求
的长。
例3. 如图，直三棱柱
中，
，侧棱
，侧面
的两条对角线交于点
，
的中点为，求证：
平面
五．课后作业： 班级 学号 姓名
1．下列关于直线
与平面
的命题中，真命题是
（ ）
若
且
，则
若
且
，则
若且，则
且
，则
2．已知直线a、b和平面M、N，且
，那么 （ ）
（A）
∥M
b⊥a （B）b⊥ab∥M
（C）N⊥Ma∥N （D）
3．在正方体中，点在侧面
及其边界上运动，并且保持
，则动点的轨迹为
（ ）
线段
线段
的中点与
的中点连成的线段 
的中点与的中点连成的线段
4．三条不同的直线，
、
、
为三个不同的平面
①若
∥
②若
∥
.
③若
、
④若
∥
上面四个命题中真命题的个数是
5．如图，
矩形所在的平面，
分别是
的中点，
（1）求证：
平面
；
（2）求证：
（3）若
，求证：
平面
6．是矩形，
，沿对角线把
折起，使
，
（1）求证：
是异面直线
与的公垂线；（2）求的长。
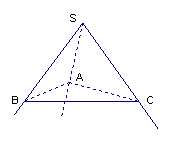7．如图，已知
是由一点
引出的不共面的三条射线，
，求证：
8．矩形中，
，平面，且
，边上存在点
，使得
，求
的取值范围。