年级:高二 科目:数学
(高二)上期期末文科数学试题
本试题分第I卷(选择题)和第II卷(非选择题)两部分,共三个大题,22个小题,总分150分,考试时间为120分钟。
第I卷(选择题,共60分)
一、选择题:(共12个小题,每小题5分。每题四个选项只有一项符合题目要求。)
1、抛物线y=-![]() 的焦点到准线的距离为( )。
的焦点到准线的距离为( )。
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、不论λ取何实数,方程x2+λy2=1所表示的曲线不可能是( )。
A、直线 B、圆 C、抛物线 D、椭圆或双曲线
3、设a,b,c是三条直线,α,β是两个不重合的平面,下面四个命题正确的是( )。
A、若a//b且a、c是异面直线,则b、c也是异面直线;
B、若a//α,b//α,则a//b;
C、若a⊥α,b//α,则a//b;
D、若a//b且a//α,b//β则α//β。
4、渐近线方程为![]() 的双曲线一定是( )。
的双曲线一定是( )。
A、![]() B、
B、![]()
C、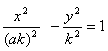 (k≠0) D、
(k≠0) D、![]() (k≠0)
(k≠0)
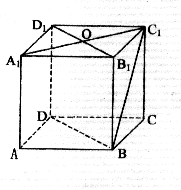
5、如图,在正方体ABCD-A1B
A、∠C1BD1 B、∠C1BO
C、∠C1BD D、∠C1BB1
6、椭圆mx2+ny2=-mn(m<n<0)的焦点为( )。
A、(0,±![]() ) B、(±
) B、(±![]() ,0)
,0)
C、(0,±![]() ) D、(±
) D、(±![]() ,0)
,0)
7、若曲线![]() (b>0)的一条准线恰好是圆x2+y2+2x=0的一条切线,则b=( )
(b>0)的一条准线恰好是圆x2+y2+2x=0的一条切线,则b=( )
A、4![]() B、4
B、4![]() C、8 D、4
C、8 D、4
8、如图,四面体ABCD中,E、F分别是AD、BC的中点,AB=1,CD=![]() ,AB⊥CD,则EF与CD,则EF与CD所成的角为( )。
,AB⊥CD,则EF与CD,则EF与CD所成的角为( )。
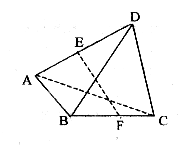
A、90° B、45°
C、60° D、30°
9、已知点P(x0,y0)在以原点为圆心的单位圆上运动,则点M(x0+y0,x0y0)的运动轨迹是( )。
A、圆 B、椭圆 C、双曲线 D、抛物线
10、如图,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于( )。
A、![]() B、1
B、1
C、2 D、4
11、若抛物线y2=2px(p>0)上三点的纵坐标的平方成等差数列,那么这三点的焦半径的关系是( )。
A、成等差数列 B、成等比数列
C、既成等差数列又成等比数列
D、既不成等差数列也不成等比数列
12、下列命题中正确的是( )。
A、若F1(m2,10)、F2(
B、若F1(m,10)、F2(m+2,10),点P满足PF1-PF2=1,则点P的轨迹为双曲线;
C、若F(1,1)、直线 l方程为mx+2my+1=0,点P到F的距离与点P到l的距离相等,则点P的轨迹为抛物线;
D、方程![]() 表示的曲线是双曲线。
表示的曲线是双曲线。
第II卷(非选择题 共90分)
二、填空题:本大题共4个小题,每小题4分,共16分
13、若双曲线![]() 的渐近线方程为y=±
的渐近线方程为y=±![]() ,则双曲线的焦点坐标为
。
,则双曲线的焦点坐标为
。
14、F1、F2分别为椭圆![]() 的左,右焦点,点P在椭圆上,且△POF2是面积为
的左,右焦点,点P在椭圆上,且△POF2是面积为![]() 的正三角形,则b2的值是
。
的正三角形,则b2的值是
。
15、已知点P(1,0),动点Q在抛物线y2=4x上移动,则PQ的最小值是 。
16、已知a,b,c,d是四条互不重合的直线,且c,d分别是a,b在平面α上的射影,给出下面两组判断:
第一组:①a⊥b ②a//b
分别从两组中各选出一个判断,使一个条件,另一个作结论,那么能写出的一个正确命题是
(填写格式:O![]() O)
O)
三、解答题:本大题共6个小题,满分共74分
17、(12分)抛物线y2=2px(p>0)与直线y=2x相交于原点O和点P,设F为抛物线的焦点,已知S△OFP=16,求抛物线的方程。
18、(12分)如图,SA⊥矩形ABCD所在平面,SA=2![]() ,AB=
,AB=![]() ,BC=7
,BC=7![]() ;
;
(1) 求直线SC与平面SAB所成的角;
(2) 求异面直线AD与SC所成的角
S
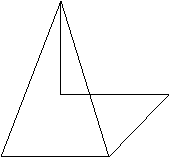
A
 D
D
B C
19、(12分)已知双曲线![]() (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e=![]() ,过
,过
点A(0,-b)和B(a,0)的直线与原点的距离为![]() 。
。
(1) 求双曲线的方程;
(2) 设点P在双曲线上,F1,F2为双曲线的左、右焦点,若
PF1+PF2=4![]() ,求Cos∠F1PF2的值。
,求Cos∠F1PF2的值。
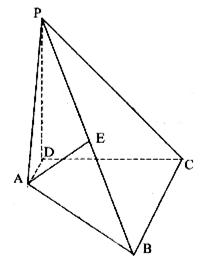
20、(12分)如图,直角梯形ABCD中,AD//BC,AD⊥DC,PD垂直于平面ABCD,且PD=DC,AD=![]() ,E为PB的中点。
,E为PB的中点。
求证:(1)AE//平面PDC
(2)AE⊥平面PBC
21、(12分)A、B、C三点是我方的三个炮兵阵地,A在B的正东,距B点
北
![]()
C

B A
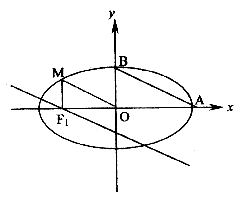
22、(14分)从椭圆![]() (a>b>0)上M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴右端点A与短轴上的端点B的连线AB//OM。
(a>b>0)上M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴右端点A与短轴上的端点B的连线AB//OM。
(1) 求椭圆的离心率;
(2) 过F1作AB的平行线交于C、D两点,若CD=3,求椭圆
的方程。