|
|
学科:数学 |
| 教学内容:6.1 不等式的性质 |
学习目的:
1.重视实数的运算性质与大小顺序之间的关系.
2.明确比较两个实数a与b的大小,就是判断它们的差a-b的符号.
3.掌握不等式的每一个性质及每一个性质的条件.
4.注意将不等式的性质与等式的性质进行类比,特别要搞清楚它们之间的区别.
方法导引:
1.比较两个实数的大小,常常利用作差法,作商法,平方作差法.
2.证明不等式的性质,常常利用比较实数大小的方法.
3.证明简单的不等式(或判断一个不等式是否正确),常常利用不等式的性质,特别要注意不等式成立的条件.
4.不等式的应用,常常将实际问题转化为不等式的相关问题,然后利用不等式的性质求解.
例题精讲:
例1 若a,b∈R+,比较![]() +
+![]() 与
与![]() +
+![]() 的大小.
的大小.
分析:作差法,作商法,平方作差法是比较两数大小的常用方法,我们在解题中要时刻记住这一条.
解法一:(作差法). ∵ a,b∈R+
∴ 〔![]() +
+![]() 〕-(
〕-(![]() +
+![]() )=
)=![]() +
+![]() -
-![]() -
-![]()
=![]() +
+![]() =(a-b)(
=(a-b)(![]() -
- ![]() )
)
=![]() =
=![]() ≥0
≥0
∴ ![]() +
+![]() ≥
≥![]() +
+![]() .
.
解法二:(作商法). ∵ a,b∈R+
∴ 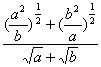 =
=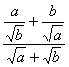
=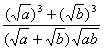 =
=![]()
=![]() ≥
≥![]() =1
=1
∴ ![]() +
+![]() ≥
≥![]() +
+![]() .
.
解法三:(平方作差法).
∵ 〔![]() +
+![]() 〕2-(
〕2-(![]() +
+![]() )2
)2
=(![]() +
+![]() +2
+2![]() )-(a+b+2
)-(a+b+2![]() )
)
=![]() -(a+b)
-(a+b)
=![]() (a2+b2-ab-ab)
(a2+b2-ab-ab)
=![]() ≥0
≥0
∴ ![]() +
+![]() ≥
≥![]() +
+![]() .
.
例2 设2<a<3,-4<b<-3,求a+b,a-b,![]() ,ab,
,ab,![]() 的取值范围.
的取值范围.
分析:运用不等式的性质解题的关键是弄清性质成立的前提条件.
解:(1)∵ 2<a<3,-4<b<-3 ∴ -2<a+b<0 (加法法则)
(2)∵ -4<b<-3 ∴ 3<-b<4 (乘法单调性)
∵ 2<a<3 ∴ 5<a-b<7 (加法法则)
(3)∵ -4<b<-3 ∴ -![]() <
<![]() <-
<-![]() (倒数法则)
(倒数法则)
∴ ![]() <-
<-![]() <
<![]() (乘法单调性) ∴
(乘法单调性) ∴ ![]() <-
<-![]() <1 (乘法法则)
<1 (乘法法则)
∴ -1<![]() <-
<-![]() (乘法单调性)
(乘法单调性)
(4)∵ 3<-b<4 ∴ 6<-ab<12 (乘法法则)
∴ -12<ab<-6 (乘法单调性)
(5)∵ 3<-b<4 ∴ 9<b2<16 (乘方法则)
∵ 2<a<3 ∴![]() <
<![]() <
<![]() (倒数法则)
(倒数法则)
∴ 3<![]() <8 (乘法法则)
<8 (乘法法则)
点评:在求解过程中要避免犯如下错误:
![]() 2<a<3
2<a<3
由 得-8<ab<-9.这是因为在运用乘法法则时不符合其前提条件.
-4<b<-3
例3 如果a>b,则下列不等式中正确的是( )
A.algx>blgx (x>0) B.ax2>bx2
C.a2>b2 D.2xa>2xb
分析:在进行不等式变形时,要注意每一步骤的理论依据是什么,切忌“随心所欲”.
解:∵ lgx∈R,当lgx<0时,由a>b
得 algx<blgx,∴ algx>blgx不成立.
x=0时,ax2=bx2=0 ∴ax2>bx2不成立.
∵ a2-b2=(a+b)(a-b) 由a>b得a-b>0,但a+b的符号不确定,∴a2>b2不成立.
∵ 2x>0 ∴2xa>2xb成立.
因此应选D.
点评:在运用不等式的性质时,乘以“数(式)”时要当心,进行“放、缩”时要当心,在“取倒”时要当心.
疑难解析:
例 已知f(x)=ax2-c 且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
分析一:要求f(3)的取值范围,因为f(1),f(2)的范围已知,故应建立f(3)关于f(1)和f(2)的关系,可通过a、c将f(3)用f(1)和f(2)表示.
解法一:∵ f(1)=a-c, f(2)=
![]() a=
a=![]()
∴
c=![]()
∴ f(3)=![]() -
-![]()
=-![]() f(1)+
f(1)+![]() f(2)
f(2)
∵ -4≤f(1)≤-1 ∴ ![]() ≤-
≤-![]() f(1)≤
f(1)≤![]()
∵ -1≤f(2)≤5 ∴ -![]() ≤
≤![]() f(2)≤
f(2)≤![]()
∴ -1≤-![]() f(1)+
f(1)+ ![]() f(2)≤20
f(2)≤20
即 -1≤f(3)≤20
分析二:建立f(3)关于f(1)和f(2)的关系时,也常用待定系数法.
解法二:令f(3)=mf(1)+nf(2)
则
即
![]()
![]() m+4n=
m+4n=![]()
∴ 解得
m+n=1
n=![]()
∴ f(3)=-![]() f(1)+
f(1)+ ![]() f(2)
f(2)
下面解法同解法一.
分析三:运用数形结合的思想方法,让问题变得直观明了.
![]() -4≤x-y≤-1
-4≤x-y≤-1
解法三:依题意,问题转化为当动点P(x,y)在满足条件
-1≤4x-y≤5
![]() -4≤x-y≤-1
-4≤x-y≤-1
的区域上变化时,求b=9x-y的取值范围.而满足条件
-1≤4x-y≤5
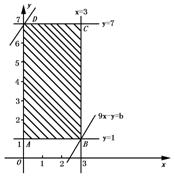
的区域是由直线x-y=-1,x-y=-4及直线4x-y=5,4x-y=-1围成的平行四边形区域(图6-1中阴影部分).
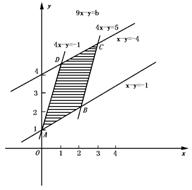
图6-1
下面考虑在直线9x-y=b平行移动过程中,当它与图6-1中阴影部分有公共点时,求b的取值范围.易知,当直线9x-y=b经过点A(0,1)时,b=9x-y取最小值9×0-1=-1,当直线9x-y=b经过点c(3,7)时,b=9x-y取最大值9×3-7=20.
∴ -1≤b≤20 即-1≤9x-y≤20
∴ -1≤f(3)≤20
注意:本题在求解过程中,常常犯这样的错误.
![]()
![]() -4≤a-c≤-1
0≤a≤3
-4≤a-c≤-1
0≤a≤3
由 求得
-1≤
从而-7≤
即 -7≤f(3)≤26.
显然,f(3)的取值范围扩大了,其扩大的原因是由满足条件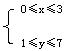 形成的区域(图6-2中阴影部分)比图6-1中所示的区域要大,所以它们表示的范围不同.
形成的区域(图6-2中阴影部分)比图6-1中所示的区域要大,所以它们表示的范围不同.
事实上,在图6-2中,当直线9x-y=b经过点D(0,7)时,b=9x-y取最小值9×0-7=-7.当直线9x-y=b经过点B(3,1)时,b=9x-y取最大值9×3-1=26.从而得到-7≤9x-y≤26.即-7≤f(3)≤26.
考点预测:
本节考点:
1.利用作差法,作商法比较两个实数的大小.
2.利用不等式的性质判断不等式的正误.
3.利用不等式的性质求变量的取值范围.
综合实践:
1、已知等比数列{an}的首项与公比均为a(-1<a<0),若bn=anlg|an|(n∈N),问是否存在自然数n0,使得对于任意n∈N都有bn≥![]() ?若存在,求出n0的值;若不存在,请说明理由.
?若存在,求出n0的值;若不存在,请说明理由.
解:∵an=a·an-1=an,∴bn=nanlg|a|.
∵-1<a<0,∴n为偶数时,bn<0,n为奇数时,bn>0,假设符合条件的n0存在,则n0必为正偶数.
∵b2k+2-b2k=(2k+2)a2k+2lg|a|-2ka2klg|a|=a2klg|a|[(2k+2)a2-2k]=![]() ],取
],取![]() 的整数部分为k0,则k<k0时,b2k+2<b2k,k=k0时,b2k+2≤b2k,k>k0时,b2k+2>b2k,∴b2>b4>…>
的整数部分为k0,则k<k0时,b2k+2<b2k,k=k0时,b2k+2≤b2k,k>k0时,b2k+2>b2k,∴b2>b4>…>![]() -2>
-2>![]() ≥
≥![]() +2,且
+2,且![]() +2<
+2<![]() +4<
+4<![]() +b<…,∴存在n0=2k0+2,
+b<…,∴存在n0=2k0+2,
使得n取所有正偶数时,bn≥![]() ,又n取奇数时,bn>0,∴bn>
,又n取奇数时,bn>0,∴bn>![]() ,从而,对任意n∈N,有bn≥
,从而,对任意n∈N,有bn≥![]() .
.
2、设0<x<1,且a>0,a≠1,试比较|loga(1-x)|与|loga(1+x)|的大小.
分析:因为a的值不确定,在解题过程中可运用换底公式去掉绝对值,也可通过平方去掉绝对值.本题可采用作差法,作商法,平方作差法比较大小.
解法一:(作差法)|loga(1-x)|-|loga(1+x)|
=![]() -
-![]() =
=![]() [|lg(1-x)|-|lg(1+x)|]
[|lg(1-x)|-|lg(1+x)|]
=![]() [-lg(1-x)-lg(1+x)]=-
[-lg(1-x)-lg(1+x)]=-![]() >0
>0
∴ |loga(1-x)||loga(1+x)|
解法二:(作商法)
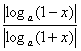 =|log(1+x)(1-x)|=-log(1+x)(1-x)
=|log(1+x)(1-x)|=-log(1+x)(1-x)
=log1+x![]() =log(1+x)
=log(1+x)![]()
=log(1+x)(1+x)-log(1+x)(1-x2)
=1-log(1+x)(1-x2)>1
∴ |loga(1-x)|>|loga(1+x)|
解法三:(平方作差法)
∵ |loga(1-x)|2-|loga(1+x)|2
=[loga(1-x)]2-[loga(1+x)]2
=[loga(1-x)+loga(1+x)][loga(1-x)-loga1+x]
=loga(1-x2)loga![]()
=lg(1-x2)lg![]() ·(
·(![]() )2
)2
∵ 0<1-x2<1 ∴ lg(1-x2)<0
又 0<![]() <1
∴lg
<1
∴lg![]() <0
<0
∴ lg(1-x2)lg![]() ·
·![]() >0
>0
∴ |loga(1-x)|>|loga(1+x)|
3、若对于某区间D内任意x1,x2,恒有f(![]() )≥
)≥![]() ,则称函数f(x)是区间D上的上凸函数,证明函数f(x)=logax (a>1)在区间(0,+∞)上是上凸函数.
,则称函数f(x)是区间D上的上凸函数,证明函数f(x)=logax (a>1)在区间(0,+∞)上是上凸函数.
分析:只需证明函数f(x)=logax满足条件.
证明:设x1,x2∈(0,+∞)
则 f(![]() )-
)-![]()
=loga![]() -
-![]() (logax1+logax2)
(logax1+logax2)
=loga![]()
=loga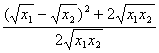
=loga[1+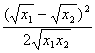 ]≥loga1=0
]≥loga1=0
∴ f(x)=logax (a>1在区间(0,+∞)上是上凸函数.
4、有甲、乙、丙三种食物的维生素A、D含量及成本如下表:
| 甲 | 乙 | 丙 | |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素D(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
某食物营养研究所想用x千克甲种食物,y千克乙种食物,z千克丙种食物配成
(1)用x,y,z表示混合物的成本C(元)
(2)确定x,y,z的值,使成本最低.
解:(1)依题意:C=11x+9y+4z 且x+y+z=100
∴ C =11x+9y+4(100-x-y)
=400+7x+5y
![]() 600x+700y+400z≥56000
600x+700y+400z≥56000
(2)依题意
800x+400y+500z≥63000
将z=100-x-y代入上方程组化简得
![]() 2x+3y≥160
2x+3y≥160
3x-y≥130
令 C=400+m(2x+3y)+n(3x-y)
![]()
![]() 2m+3n=7 m=2
2m+3n=7 m=2
则 ∴
3m-n=5 n=1
∴ C=400+2(2x+3y)+(3x-y)≥400+2×160+130=850
![]()
![]() 2x+3y=160
x=50
2x+3y=160
x=50
当且仅当 即 时等号成立.
3x-y=130 y=20
此时 z=100-50-20=30
因此,当x=50千克,y=20千克,z=30千克时成本最低,为850元.

【同步达纲练习】
知识强化:
一、选择题
1.下列命题正确的是( )
A.若a>b,则ac2>bc2 B.若a>b,c>d,则ac>bd
C.若![]() >
>![]() ,则a>b
D.若a>b,ab>0,则
,则a>b
D.若a>b,ab>0,则![]() <
<![]() .
.
2.设a<b<0,则下列不等式中不成立的是( )
A. ![]() >
>![]() B.
B.![]() >
>![]()
C.|a|>|b| D.a2>b2
3.若a=log0.20.3,b=log0.30.2,c=1,则a、b、c的大小关系是( )
A.a>b>c B.b>a>c
C.b>c>a D.c>b>a
4.“a+b>2c”的一个充分条件是( )
A.a>c或b>c B.a>c且b>c
C.a>c或b<c D.a>c或b<c
5.若a<0,-1<b<0,则下列不等式中正确的是( )
A.a>ab>ab2 B.ab2>ab>a
C.ab>a>ab2 D.ab>ab2>a
二、填空题
6.若a>b>c>0,则![]() ,
,![]() ,
,![]() ,c从小到大的顺序是____________________.
,c从小到大的顺序是____________________.
7.已知12<m<60,15<n<36,则![]() 的取值范围是_________________.
的取值范围是_________________.
8.若a,b∈R,给出下列条件:(1)a+b>1,(2)a+b=2,(3)a+b>2,(4)a2+b2>2,(5)ab>1,其中能推出“a,b中至少有一个数大于1”的条件是______________.
三、解答题
9.已知-1<a<1,比较(1-![]() )与(
)与(![]() -1)的大小.
-1)的大小.
10.已知![]() <α<β<π,求2α-3β的取值范围.
<α<β<π,求2α-3β的取值范围.
素质优化:
1.若a>b>c,a+b+c=0,则下面不等式中恒成立的是( )
A.ab>ac B.ac>bc
C.a|b|>|b|c D.a2>b2>c2
2.若a,b,∈R,则ab(a-b)>0成立的一个充要条件是( )
A.0<![]() <
<![]() B.0<
B.0<![]() <
<![]()
C.![]() <
<![]() D.
D. ![]() <
<![]()
3.若a+d=b+c,|a-d|<|b-c|则ad与bc的关系是( )
A.ad=bc B.ad<bc
C.ad>bc D.ad与bc的大小不确定
4.已知0<a<b<1,则ab,logba,![]() 的大小关系是 ( )
的大小关系是 ( )
A. ![]() <ab<logba B.
<ab<logba B. ![]() <logba<ab
<logba<ab
C.logba<![]() <ab
D.ab<
<ab
D.ab<![]() <logba
<logba
5.若a<b<0,则下列结论中正确的是( )
A.不等式![]() >
>![]() 与
与![]() >
>![]() 均成立.
均成立.
B.不等式![]() >
>![]() 与
与![]() >
>![]() 均不成立.
均不成立.
C.不等式![]() >
>![]() 与(a+
与(a+![]() )2>(b+
)2>(b+![]() )2均不成立.
)2均不成立.
D.不等式![]() >
>![]() 与(a+
与(a+![]() )2>(b+
)2>(b+![]() )2均不成立.
)2均不成立.
二、填空题
6.以下四个不等式:(1)a<0<b
(2)b<a<0
(3)b<0<a
(4)0<b<a,其中使![]() <
<![]() 成立的充分条件是____________.
成立的充分条件是____________.
7.若a,b,m∈R+,且![]() <
<![]() ,则a与b的大小关系是_____________.
,则a与b的大小关系是_____________.
8.设f(x)=ax2+b (a≠0)且0≤f(0)≤1,2≤f(2)≤3,则f(3)的取值范围是_______.
三、解答题
9.设实数a,b,c满足①b+c=6-4a+3a2,②c-b=4-4a+a2,试确定a,b,c的大小关系.
10.已知-3<a<2,![]() <b≤2a,c=b-2a,求c的取值范围.
<b≤2a,c=b-2a,求c的取值范围.
创新深化:
一、选择题
![]()
![]() 2<a+b<4
0<a<1
2<a+b<4
0<a<1
1.设甲:a和b满足 ,乙:a和b满足 ,那么( )
0<ab<3 2<b<3
A.甲是乙的充分但不必要条件.
B.甲是乙的必要但不充分条件.
C.甲是乙的充要条件.
D.甲不是乙的充分条件,也不是乙的必要条件.
2.已知x∈R+,x≠1,P=(1+![]() )3,Q=
)3,Q=![]() ,则P与Q的大小关系是( )
,则P与Q的大小关系是( )
A.P>Q B.P=Q
C.P<Q D.不能确定
3.设f(x)=|lgx|,若0<a<b<c,且f(a)>f(c)>f(b),则下列命题成立的是( )
A.(a-1)(c-1)>0 B.ac>1
C.ac=1 D.ac<1
4.已知a,b,c,d∈R,且满足①d>c ②a+b=c+d ③a+d<b+c,则下面不等式中正确的是( )
A.d>b>a>c B.b>c>d>a
C.b>d>c>a D.b>d>a>c
5.设a=sin15°+cos15°,b=sin16°+cos16°,则下面不等式中正确的是( )
A.a<![]() <b
B.a<b<
<b
B.a<b<![]()
C.b<a<![]() D.b<
D.b<![]() <a
<a
二、填空题
6.已知a,b,m,n∈R+,且m+n=1,则![]() 和m
和m![]() +m
+m![]() 的大小关系是_______.
的大小关系是_______.
7.若0<a<b,且a+b=1,则a,b,![]() ,2ab,a2+b2从小到大的顺序是_______.
,2ab,a2+b2从小到大的顺序是_______.
8.已知“a>b,a-![]() >b-
>b-![]() ”同时成立,则ab应满足的条件是_______.
”同时成立,则ab应满足的条件是_______.
三、解答题
9.已知实数a,b,c满足![]() +
+![]() +
+![]() =0,其中m∈R+,设f(x)=ax2+bx+c(a≠0).证明:af(
=0,其中m∈R+,设f(x)=ax2+bx+c(a≠0).证明:af(![]() )<0
)<0
10.在等差数列{an}和等比数列{bn}中,a1=b1>0,a3=b3>0,a1≠a3.试比较下面两组数的大小.
(1) a2与b2.
(2) (2)a5与b5.

参考答案:
知识强化:
1.D 2.B
3.C 4.B 5.D
6.C,![]() ,
, ![]() ,
, ![]() 7.(
7.(![]() ,4) 8.③ 9.∵(1-
,4) 8.③ 9.∵(1-![]() )=
)=![]() =
=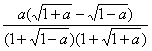
=![]() ≥0 ∴1-
≥0 ∴1-![]() ≥
≥![]() -1
-1
10.∵![]() <α<π ∴π<2α<2π
∵
<α<π ∴π<2α<2π
∵![]() <β<π ∴-2π<-2β<-π ∴-π<2α-2β<π 又α<β
∴α-β<0 ∴-π<2α-2β<0,又-π<-β<-
<β<π ∴-2π<-2β<-π ∴-π<2α-2β<π 又α<β
∴α-β<0 ∴-π<2α-2β<0,又-π<-β<-![]() ,∴-2π<2α-3β<-
,∴-2π<2α-3β<-![]()
素质优化:
1.A 2.C 3.C
4.A 5.B 6.①②④ 7.b<a 8.[![]() ]
]
9.∵c-b=(a-2)2≥0,∴c≥b,又2b=2+2a2,∴b=1+a2,∴b-a=a2-a+1=(a-![]() )2+
)2+![]() >0,∴b>a,从而c≥b>a.
>0,∴b>a,从而c≥b>a.
10.∵-3<a<2,∴-4<-2a<6,∴b-4<b-2a<b+6,又![]() <b,∴
<b,∴![]() -4<b-4,∵b≤2a,∴b+6≤2a+6,∴
-4<b-4,∵b≤2a,∴b+6≤2a+6,∴![]() -4<c<2a+6,∵a>-3,∴
-4<c<2a+6,∵a>-3,∴![]() -4>-5,又a<2,∴2a+b<10,∴-5<c<10
-4>-5,又a<2,∴2a+b<10,∴-5<c<10
创新深化:
1.B 2.A 3.D 4.C 5.B
6.![]() ≥m
≥m![]() +n
+n![]() 7.a,2ab,
7.a,2ab,![]() ,a2+b2,b 8.ab>0或ab<-1 9.∵af(
,a2+b2,b 8.ab>0或ab<-1 9.∵af(![]() )=a[a(
)=a[a(![]() )2+b(
)2+b(![]() )+c]=am[
)+c]=am[![]() ]=am[
]=am[![]() ]=
]=![]() <0
10.设an=a1+(n-1)d,bn=a1qn-1,依题意a1+2d=a1q2,∴d=
<0
10.设an=a1+(n-1)d,bn=a1qn-1,依题意a1+2d=a1q2,∴d=![]() a1q2-
a1q2-![]() a1,∴(1)a2-b2=a1+d-a1q=a1-a1q+
a1,∴(1)a2-b2=a1+d-a1q=a1-a1q+![]() aq2-
aq2-![]() a=
a=![]() aq2-a1q+
aq2-a1q+![]() =
=![]() a(q-1)2,∵a1≠a3,∴a1≠a1+2d,即d≠0,3q≠1,∴a2-b2=
a(q-1)2,∵a1≠a3,∴a1≠a1+2d,即d≠0,3q≠1,∴a2-b2=![]() a(q-1)2>0,∴a2>b2.(2)a5-b5=a1+4d-a1q4=a1-a1q4+2a1q2-2a1=-a1q4+2a1q2-a1=-a1(q2-1)2<0,∴a5<b5.
a(q-1)2>0,∴a2>b2.(2)a5-b5=a1+4d-a1q4=a1-a1q4+2a1q2-2a1=-a1q4+2a1q2-a1=-a1(q2-1)2<0,∴a5<b5.
