|
|
学科: 数学 |
| 教学内容:6.4 不等式的解法 |
【基础知识精讲】
1.解不等式的基本思想
我们已学过的一元一次不等式、一元二次不等式的解法是学习本节的基础.在解其它类型的不等式时,通过转化,将它们等价变形为一次、二次不等式(组).转化思想为:如果不等式是超越不等式,则把它等价变形为代数不等式;如果代数不等式是无理不等式,则把它等价变形为有理不等式;如果有理不等式是分式不等式,则把它等价变形为整式不等式;如果整式不等式是高次不等式,则把它等价变形为一次、二次不等式(组).
注意:每一步变形,都应是不等式的等价变形.
2.不等式的解法
①一元一次不等式的解法
一元一次不等式ax>b的解集情况是:
1°当a>0时,解集为{x|x>![]() }
}
2°当a<0时,解集为{x|x<![]() }
}
3°当a=0时, b≥0时,解集为![]()
b<0时,解集为R.
②一元二次不等式的解法:
设a>0,x1,x2是方程.
![]() ax2+bx+c=0的两实根,且x1<x2,则一元二次不等式的解集如下表所示:
ax2+bx+c=0的两实根,且x1<x2,则一元二次不等式的解集如下表所示:
| 类型 解集 | ax+bx+c>0 | ax2+bx+c≥0 | ax2+bx+c<0 | ax2+bx+c≤0 |
| Δ>0 | {x|x<x1或x>x2} | {xx≤x1或x≥x2} | {x|x1<x<x2} | {x|x1≤x≤x2} |
| Δ=0 | {x|x≠- x∈R} | R |
| {x|x=- |
| Δ<0 | R | R |
|
|
注:当a<0时,可在不等式两边乘-1转化为二次项系数为正的情况,再按上表进行.
③高次不等式的解法:
高次不等式用根轴法求解,其步骤是:
1°将f(x)的最高次项的系数化为正数.
2°将f(x)分解为若干个一次因式的积.
3°将每一个一次因式的根标在数轴上,从右上方依次穿过每一个根点画曲线.
4°根据曲线显现出f(x)的符号变化规律,写出不等式的解集.
④分式不等式的解法:
先将不等式整理成![]() >0或
>0或![]() ≥0的形式,再转化为整式不等式求解.
≥0的形式,再转化为整式不等式求解.
即 ![]() >0
>0![]() f(x)·g(x)>0
f(x)·g(x)>0
![]() ≥0
≥0![]()
![]()
⑤无理不等式的解法:转化为有理不等式求解.
![]() >g(x)
>g(x) ![]()
![]() 或
或![]()
![]() <g(x)
<g(x) ![]()
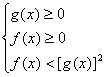
![]() >
>![]()
![]()
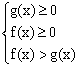
![]() f(x)>g(x)≥0
f(x)>g(x)≥0
⑥指数不等式的解法.
1°同底法
af(x)>ag(x)![]()
![]()
2°取对数法
af(x)>bg(x)![]()
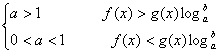
3°换元法
![]()
⑦对数不等式的解法.
1°同底法
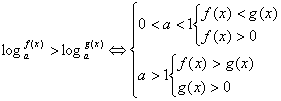
2°换元法
![]()
3.本节学习要求
(1)解各种变型的不等式,关键要把它们变形为一次、二次不等式(组).
(2)求函数的定义域、值域、二次方程的根的分布、讨论参变量的取值范围等均可化为解不等式的问题.
通过本节学习,培养学生的运算能力,使学生理解掌握等价转化的致学思想方法.
【重点难点解析】
知识的学习应遵循人类的认识规律和知识本身的渐近性、逻辑性.因此,建议同学们在学习本节时,应复习初中的一元一次不等式、一元二次不等式的解法,在此基础上,继续学习高次不等式、分式不等式、无理不等式、指数不等式及对数不等式的解法.
例1 解关于x的不等式:![]() >1 (a≠1)
>1 (a≠1)
分析 这是一个分式不等式,应先移项,再通分进行因式分解变形.切忌两边同乘以(x-2)而转化为整式不等式,因为(x-2)的正负未知.另外,注意对参数a的正确的分类讨论.
解:原不等式等价于![]() >0
>0
即为 ![]() >0
>0
![]() [(a-1)x-(a-2)](x-2)>0
[(a-1)x-(a-2)](x-2)>0
![]() (a-1)(x-
(a-1)(x-![]() )(x-2)>0 ①
)(x-2)>0 ①
当a>1时,式①![]() (x-
(x-![]() )(x-2)>0
)(x-2)>0
∵ ![]() -2=-
-2=-![]() -1<0
-1<0
∴ ![]() <2.
<2.
∴ 原不等式的解集为(-∞,![]() )∪(2,+∞).
)∪(2,+∞).
当a<1时,式①![]() (x-
(x-![]() )(x-2)<0
)(x-2)<0
由 2-![]() =
=![]() 知
知
当0<a<1时,![]() >2,则原不等式解集为(2,
>2,则原不等式解集为(2,![]() )
)
当a=0时,原不等式(x-2)2<0,解集为![]() .
.
当a<0时,![]() <2,则原不等式解集为(
<2,则原不等式解集为(![]() ,2).
,2).
综上所述:
当a<0时,原不等式解集为(![]() ,2)
,2)
当a=0时,原不等式解集为![]() .
.
当0<a<1时,原不等式解集为(2,![]() )
)
当a>1时,原不等式解集为(-∞,![]() )∪(2,+∞)
)∪(2,+∞)
点评:本题需要两级分类,第一级按a>1和a<1分为两级,多数学生都能做到,在a<1的情况下,又要按两根![]() 与2的大小关系分为a<0,a=0和0<a<1三类,这时就有不少学生找不到分类的依据,甚至缺乏分类讨论的意识.
与2的大小关系分为a<0,a=0和0<a<1三类,这时就有不少学生找不到分类的依据,甚至缺乏分类讨论的意识.
例2 解不等式![]() <x
<x
分析 此题是分式不等式,可按分式不等式的解法求解.即需先移项通分,整理成![]()
![]() 0的形式,再转化为它们的整式不等式求解.
0的形式,再转化为它们的整式不等式求解.
解:移项整理,将原不等式转化为:
![]() >0
>0
∵ x2+x+1>0恒成立.
∴ 原不等式等价于![]() >0
>0
解之,得原不等式解集为{x|-1<x<2或x>3}.
注:此题也可用列表法或数轴标根法求解,但用根轴法更简捷.
例3 解不等式log2![]() ·log
·log![]()
![]() >-2.
>-2.
分析 此题为对数不等式,(可通过换元),由log![]()
![]() =
=![]()
![]() =-1-log2
=-1-log2![]() ,所以可通过换元令t=log2
,所以可通过换元令t=log2![]() ,则可转化为代数不等式求解.
,则可转化为代数不等式求解.
解:原不等式可化为:
log2![]() ·[-1-log2
·[-1-log2![]() ]>-2
]>-2
令log2![]() =t,则上面不等式可化为:
=t,则上面不等式可化为:
t(-1-t)>-2.即t2+t-2<0
即 (t+2)(t-1)<0
∴ -2<t<1
从而有 -2<log2![]() <1
<1
则 2-2<2x-1<2
即 ![]() <2x<3
<2x<3
∴ log2![]() <x<log23
<x<log23
∴ log25-2<x<log23
∴ 原不等式解集为{x|log25-2<x<log23}
【难题巧解点拨】
例1 关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有解,求实数m的取值范围.
分析 此题为含参的一元二次方程解的情况,可由二次方程的实根分布来解.
则可设f(x)=x2+(m-1)x+1
题意即为f(x)=0在[0,2]上有解,其中包括两种情况:1°有一解,2°有两解.
解:设f(x)=x2+(m-1)x+1 x∈[0,2],则:
(1)f(x)=0在区间[0,2]上有一解:
因为f(0)=1>0
所以只需f(2)≤0
即 4+2(m-1)+1≤0![]() m≤-
m≤-![]()
(2)f(x)=0在区间[0,2]上有二解.
则有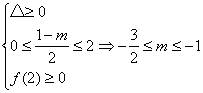
综上由(1)(2)可知:m≤-1.
例2 若关于x的方程4x+a·2x+a+1=0有实数解,求实数a的取值范围?
解法一:令t=2x(t>0),则原方程化为t2+at+a+1=0(1)
则问题转化为方程(1)在(0,+∞)上有实数解,求a的取值范围.
由 即
即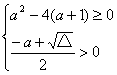
解得:a≤2-2![]()
解法二:令t=2x(t>0),则原方程化为
t2+at+a+1=0,变形为:
a =-![]() =-
=-![]()
=-[(t-1)+ ![]() ]
]
=-[(t+1)+ ![]() -2]≤-(2
-2]≤-(2![]() -2)=2-2
-2)=2-2![]()
例3 已知f(x)是定义在区间(-∞,4)上的减函数,是否存在实数m,使得
f(m-sinx)≤f(![]() -
-![]() +cos2x)对定义域内的一切实数x均成立.若存在,求出m的取值范围,若不存在,说明理由.
+cos2x)对定义域内的一切实数x均成立.若存在,求出m的取值范围,若不存在,说明理由.
解:假设存在实数m,依题意得
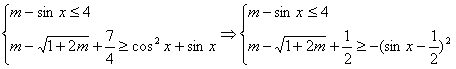
∵sinx的最小值为-1,且-(sinx-![]() )2的最大值为0,要满足题意,则须有:
)2的最大值为0,要满足题意,则须有:
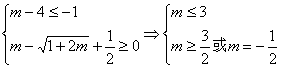
∴m的取值范围是{m|m=![]() 或
或![]() ≤x≤3}
≤x≤3}
【命题趋势分析】
平时要求:1.按解各类不等式的解法来求解不等式.
2.含参的不等式问题,能对参数进行正确的分类讨论.
3.应用不等式可求函数的定义域、值域、讨论函数的单调区间、讨论函数的一元二次方程根的存在和根的分布.
【典型热点考题】
例1 实数m在什么范围时方程x2+(m-3)x+m=0的两根满足:(1)都是正根;(2)都在(0,2)内.
解:(1)依题意,满足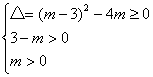 时,即m∈(0,1)时两根均为正.
时,即m∈(0,1)时两根均为正.
(2)设f(x)=x2+(m-3)x+m,则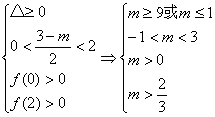
![]()
![]() <m≤1,即m∈(
<m≤1,即m∈(![]() ,1)时,两根都在(0,2)内.
,1)时,两根都在(0,2)内.
例2 关于实数x的不等式|x-![]() (a+1)2|≤
(a+1)2|≤![]() (a-1)2与x2-3(a+1)x+2(
(a-1)2与x2-3(a+1)x+2(![]() B的a的取值范围.
B的a的取值范围.
解:由|x-![]() (a+1)2|≤
(a+1)2|≤![]() (a+1)2得
(a+1)2得
由x2-3(a+1)x+2(
可得(x-2)[x-(![]() 时,B={x|2≤x≤
时,B={x|2≤x≤
当![]() 时,B={x|
时,B={x|
∴当a≥![]() 时,若A
时,若A![]() B,则有
B,则有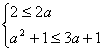 ,解不等式组得1≤a≤3.
,解不等式组得1≤a≤3.
当a<![]() 时,若A
时,若A![]() B,则有
B,则有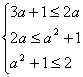 ,解不等式组得:a=-1,
,解不等式组得:a=-1,
故使A![]() B的a的取值范围是{a|1≤a≤3或a=-1}.
B的a的取值范围是{a|1≤a≤3或a=-1}.
例3 设y=![]() (a>0,b>0),求使y为负值的x的取值范围.
(a>0,b>0),求使y为负值的x的取值范围.
解:要y<0,只要a2x+2(ab)x-b2x>0,即b2x[(![]() )2x+2·(
)2x+2·(![]() )x-1]>0,
)x-1]>0,
∵b2x>0,∴[(![]() )x]2+2(
)x]2+2(![]() )x-1>0.
)x-1>0.
解这个关于(![]() )x的二次不等式得:(
)x的二次不等式得:(![]() )x>
)x>![]() -1或(
-1或(![]() )x<-
)x<-![]() -1,但(
-1,但(![]() )x>0,
)x>0,
∴只有(![]() )x>
)x>![]() -1,
-1,
∴当a=b>0时,x∈R.
当a>b>0时,![]() >1,两边取以
>1,两边取以![]() 为底的对数,得x>
为底的对数,得x>![]() .
.
当0<a<b时,0<![]() <1,两边取以
<1,两边取以![]() 为底的对数,得x<
为底的对数,得x<![]() ,
,
因此x的取值范围是:当a=b>0时,x∈R.当a>b>0时,x∈(![]() ,+∞).
,+∞).
当0<a<b时,x∈(-∞,![]() ).
).

【同步达纲练习】
A
一、选择题
1.若x满足![]() <2与
<2与![]() >-3则x的取值范围是( )
>-3则x的取值范围是( )
A. -![]() <x<
<x<![]() B .x>
B .x>![]()
C. x<-![]() D. 0<x<
D. 0<x<![]()
2.函数y=![]() 的定义域为( )
的定义域为( )
A.{x|x≥-3} B.{x|-3≤x≤![]() }
}
C.{x|1≤x<![]() D.{x|x≥-1}
D.{x|x≥-1}
3.与不等式![]() ≥0同解的不等式是( )
≥0同解的不等式是( )
A.(x-5)(4-x)≥0 B.lg(x-4)≤0
C. ![]() ≥0 D.lg(x-5)≥0
≥0 D.lg(x-5)≥0
4.设0<a<1,给出下面四个不等式:
①![]() <
<![]() ②
②![]() >(
>(![]() )a
)a
③(![]() )a >aa ④aa>
)a >aa ④aa>![]()
其中不成立的有( )
A.0个 B.1个 C.2个 D.3个
5.已知方程mx2-2(m+2)x+(m+5)=0有两个不同的正根,则m的取值范围是( )
A.m<4 B.0<m<4
C.m<-5或0<m<4 D.m<-2或0<m<4
二、填空题
6.不等式![]() ≥x的解集为
.
≥x的解集为
.
7.不等式(![]() )
)![]() >3-2x的解集为
.
>3-2x的解集为
.
8.不等式lg![]() <1的解集为
.
<1的解集为
.
三、解答题
9.若不等式![]() <0的解集为R,求实数m的取值范围.
<0的解集为R,求实数m的取值范围.
10.解不等式lg![]() <0
<0
AA级
一、选择题
1.已知I=R,集合M={x|![]() ≤0,x∈R},N={x|(x-2000)(x-2001)≥0,x∈R},P={x|10(x-2000)(x-2001)≥1,x∈R},则( )
≤0,x∈R},N={x|(x-2000)(x-2001)≥0,x∈R},P={x|10(x-2000)(x-2001)≥1,x∈R},则( )
A.![]() ∩N=P
B.M∪P=N
∩N=P
B.M∪P=N
C.M∩N∪P=M D.M∪N∪P=R
2.已知不等式x2-4x+3<0① x2-6x+8<0② 2x2-9x+m<0③,要使同时满足①②的x也满足③,则有( )
A.m>9 B.m=
3.若函数f(x)=![]() 的值域为(-∞,+∞),则实数k的取值范围是( )
的值域为(-∞,+∞),则实数k的取值范围是( )
A.(-2![]() ,2
,2![]() )
B.[-2
)
B.[-2![]() ,2
,2![]() ]
]
C.(-∞,-2![]() )∪(2
)∪(2![]() ,+∞) D.(-∞,-2
,+∞) D.(-∞,-2![]() )∪[2
)∪[2![]() ,+∞]
,+∞]
4.关于x的不等式(k2-2k+![]() )x<(k2-2k+
)x<(k2-2k+![]() )1-x的解集为( )
)1-x的解集为( )
A.{x|x<![]() } B.{x|x>
} B.{x|x>![]() }
}
C.{x|x>2} D.{x|x<2}
5.若ax2+bx+c>0的解集为{x|x<-2或x>4},那么对于函数f(x)=ax2+bx+c会有( )
A.f(5)<f(2)<f(-1) B.f(2)<f(5)<f(-1)
C.f(-1)<f(2)<f(5) D.f(2)<f(-1)<f(5)
二、填空题
6.不等式组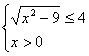 的解集是
.
的解集是
.
7.不等式ax2+bx+2>0的解集为(-![]() ,
,![]() ),则a+b的值是
.
),则a+b的值是
.
8.4x(x+2)-8·32x>0的解集为 .
三、解答题
9.已知A={x|5-x≥2![]() }
}
B={x|x2-ax≤x-a},当A![]() B时,求a的取值范围.
B时,求a的取值范围.
10.设关于x的二次方程px2+(p-1)x+p+1=0有两个不等的正根,且其中一根大于另一根的两倍,求p的取值范围.
【素质优化训练】
一、选择题
1.如果不等式![]() ≥x的解集在数轴上构成长度为
≥x的解集在数轴上构成长度为
A.1
B
2.设命题P:关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同;命题Q:![]() =
=![]() =
=![]() ,则命题Q是命题P的( )
,则命题Q是命题P的( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.设x1<x2…<xn,n∈N且n≥2.{x|(x-x1)(x-x2)…(x-xn)>0}![]() {x|x2-(x1+xn)x+x1xn>0},则n( )
{x|x2-(x1+xn)x+x1xn>0},则n( )
A.等于2 B.是大于2的任意奇数
C.是大于2的任意偶数 D.是大于1的任意自然数
4.在x∈(![]() ,3)上恒有|logax|<1成立,则实数a的取值范围是( )
,3)上恒有|logax|<1成立,则实数a的取值范围是( )
A.a≥3 B.0<a≤![]()
C.a≥3或0<a≤![]() D.a≥3或0<a<
D.a≥3或0<a<![]()
5.已知f(x)、g(x)都是奇函数,f(x)>0的解集为(a2-b),g(x)>0的解集为(![]() ,b),则f(x)·g(x)>0的解集为( )
,b),则f(x)·g(x)>0的解集为( )
A.(![]() ,
,![]() )
B.(-b,-a2)
)
B.(-b,-a2)
C.(a2,
![]() )∪(-
)∪(-![]() ,-a2) D.(
,-a2) D.(![]() ,b)∪(-b2,-a2)
,b)∪(-b2,-a2)
二、填空题
6.若关于x的不等式组![]() 的解集不是空集,则实数a的取值范围是 .
的解集不是空集,则实数a的取值范围是 .
7.设函数f(x)=![]() ,x∈(-∞,+∞)的最大值为4,最小值为-1,则a、b的值为 .
,x∈(-∞,+∞)的最大值为4,最小值为-1,则a、b的值为 .
8.已知函数f(x)=ax+2a+1的值在-1≤x≤1时有正有负,则a的取值范围为 .
三、解答题
9.已知F(x)=f(x)-g(x),其中f(x)=loga(x-b),当且仅当点(x0,y0)在f(x)的图像上时,点(2x0,2y0)在y=g(x)的图像上.(b>0,a>0且a≠1)
(1)求y=g(x)的解析式. (2)当F(x)≥0时,求x的范围.
10.汽车在行驶过程中,由于惯性作用,刹车时还要继续向滑行一段距离才能停住,称这段距离为刹车距离,刹车距离是分析事故的一个重要因素,在一个限速为40千米/小时以内的弯道上,甲、乙两辆汽车相向而行,发现情况不对时,同时刹车,但还是相撞了.事故后,现场测得甲车的刹车距离是略超过12米,乙车的距离略超过10米,又已知甲、乙两种车型刹车距离s米与车速x千米/小时之间有如下关系:S甲=0.1x+0.01x2,S乙=0.05+0.005x2,问超速应负责任的是谁?

答案:
A级
1.D 2.C 3.B 4.B 5.B
6.{x|x≤![]() } 7.{x|-2<x<4} 8.{x|-4<x<2}
} 7.{x|-2<x<4} 8.{x|-4<x<2}
9.解:∵x2-8x+20=(x-4)2+4>0恒成立,∴原不等式等价于mx2+2(m+1)x+9m+4<0恒成立,则只须![]() 即
即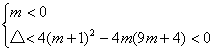 ,于是可得m∈(-∞,-
,于是可得m∈(-∞,- ![]() ).
).
10.解:由对数函数的性质和定义知:0<x-![]() <1,即0<
<1,即0<![]() <1,则
<1,则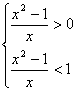 即
即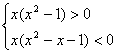 ,当x>0时,有
,当x>0时,有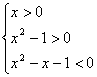 ,∴解集为{x|1<x<
,∴解集为{x|1<x<![]() },当x<0时,有
},当x<0时,有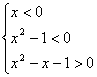 ,∴解集为{x|-1<x<
,∴解集为{x|-1<x<![]() },∴原不等式解集为{x|-1<x<
},∴原不等式解集为{x|-1<x<![]() }∪{x|1<x<
}∪{x|1<x<![]() }.
}.
AA级
1.D 2.C 3.D 4.A 5.D
6.[3,5] 7.-14 8.{x|x>![]() 或x<-1}
或x<-1}
9.解:A={x|1≤x≤3},B={x|(x-a)(x-1)≤0},要使A![]() B,则只需a>3即可,故a的取值范围为a>3.
B,则只需a>3即可,故a的取值范围为a>3.
10.解:方程有两不等正根的充要条件是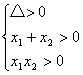 ,即
,即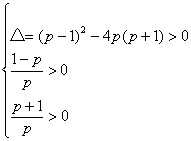 解得:0<p<
解得:0<p<![]() -1,证x1=
-1,证x1=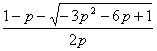 ,x2=
,x2=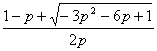 ,由x2>2x1并注意p>0得:3
,由x2>2x1并注意p>0得:3![]() >1-p>0,∴28p2+52p-8<0,即7p2+13p-2<0,∴-2<p<
>1-p>0,∴28p2+52p-8<0,即7p2+13p-2<0,∴-2<p<![]() ,综上得p的取值范围为{P|0<p<
,综上得p的取值范围为{P|0<p<![]() }.
}.
【素质优化训练】
1.B 2.D 3.C 4.C 5.C
6.a>-1 7. ![]() 或
或![]() 8.-1<a<-
8.-1<a<-![]()
9.解:(1)易知y0=loga![]() ,令2x0=u,2y0=v,则x0=
,令2x0=u,2y0=v,则x0=![]() ,y0=
,y0=![]() 代入得v=2loga
代入得v=2loga![]() ,又因为点(u、v)在y=g(x)图象上,∴y=g(x)=2loga
,又因为点(u、v)在y=g(x)图象上,∴y=g(x)=2loga![]() .
.
(2)F(x)=f(x)-g(x)=loga![]() -2loga
-2loga![]() ,由F(x)≥0得loga
,由F(x)≥0得loga![]() -2loga
-2loga![]() ≥0 ①,当a>1时,不等式①等价于
≥0 ①,当a>1时,不等式①等价于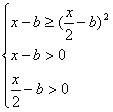
![]()
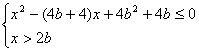
![]()
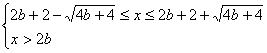
![]() 2b<x≤2b+2+2
2b<x≤2b+2+2![]() .当0<a<1时,不等式①等价于
.当0<a<1时,不等式①等价于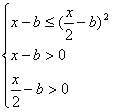
![]() x≥2b+2+2
x≥2b+2+2![]() ,∴当a>1,2b<x≤2b+2+2
,∴当a>1,2b<x≤2b+2+2![]() 时F(x)≥0,当0<a<1,x≥2b+2+2
时F(x)≥0,当0<a<1,x≥2b+2+2![]() 时,F(x)≥0.
时,F(x)≥0.
10.解:依题意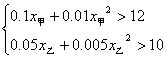
![]() 由①解得x甲<-40或x甲>30,由②解得x乙<-50或x乙>40,∴乙车超速,应负事故的主要责任.
由①解得x甲<-40或x甲>30,由②解得x乙<-50或x乙>40,∴乙车超速,应负事故的主要责任.
