不等式测试训练（B1）
班级 姓名 编号
一、选择题（本大题共12小题，每小题6分，共72分）
1、 下列不等式不成立的是 （ ）
A、
B、
C、
D、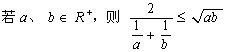
2、若
，则下列不等式中成立的是 （ ）
A、
B、
C、
D、
3、已知
，则下列不等式中成立的是
（ ）
4、下列不等式中解集为实数集R的是
5、不等式
的解集为
6、
（ ）
A、充分但年必要条件 B、必要但不充分条件
C、充要条件 D、既不充分也不必要条件
7、设
则
中最小的是
（ ）
8、 不等式
的取值范围是
（ ）
9、如果方程
的两个实根一个小于‒1，另一个大于1，那么实数m的取值范围是
（ ）
10、如果
的取值范围是 （ ）
11、在
三个结论：①
，②
③
，其中正确的个数是
（ ）
A、0 B、1 C、2 D、3
12、设
（ ）
A、
B、
C、
D、以上都不对
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（本大题共4小题，每小题6分，共24分）
13、
14、
15、若直角三角形的斜边长为1，则其内接圆半径的最大值为 ；
16、若
的大小关系是_________________。
三、解答题（本大题共4小题，共54分。）
17、（12分）设
18、（14分）设
求关于
不等式
的解集。
19、（14分）解关于
。
20、（14分）某单位准备建造一间面积为
的背面靠墙的矩形平顶房屋，房屋墙的高度为4m，房屋正面的造价为800元/m2，房屋的侧面的造价为600元/m2， 屋顶的造价为1000元/m2.若不计房屋背面的费用,问怎样设计房屋能使造价最底,最底造价是多少元？
 |
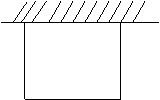四.选做题: （另加5分）已知：函数
在R上是增函数，
。
（1）、求证：如果
；
（2）、判断（1）中的命题的逆命题是否成立？并证明你的结论。
不等式单元测试卷答案
一、选择题（本大题共12小题，每小题6分，共72分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | B | D | C | D | A | C | D | B | D | D |
二、填空题（本大题共4小题，每小题6分，共24分）
13、
；
14、
15、若直角三角形的斜边长为1，则其内切圆半径的最大值为
；
16、若的大小关系是 
（当且仅当
取等号）。
三、解答题（本大题共4小题，共54分。）
17、（12分）设
解：
即
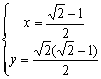时取等号，
18、（14分）设求关于不等式的解集。
解：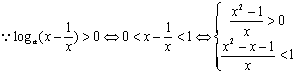
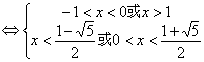
所以所求的不等式的解集为
解法二：
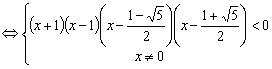
所以所求的不等式的解集为
19、（14分）解关于。
解： 
，
；
，
；
，
。
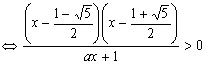
所以，
，不等式的解集是
；
，不等式的解集是
；
，不等式的解集是
。
20、（14分）某单位准备建造一间面积为的背面靠墙的矩形平顶房屋，房屋墙的高度为4m，房屋正面的造价为800元/m2，房屋的侧面的造价为600元/m2， 屋顶的造价为1000元/m2.若不计房屋背面的费用,问怎样设计房屋能使造价最底,最底造价是多少元？
解:设房屋的长为
则宽为
,正面墙的面积为
两侧面面积和为
,房屋的总造价为
,当且仅当
答：使房屋的的长为
时，房屋的造价最低，最低造价为
四.选做题: （另加5分）已知：函数在R上是增函数，。
（1）、求证：如果；
（2）、判断（1）中的命题的逆命题是否成立？并证明你的结论。
（1）.证明：∵
,而函数在R上是增函数，
,从而
.
(2). 解: （1）中的命题的逆命题是:
它是成立.
下面给出证明: (用反证法)假设
从而
,而函数在R上是增函数，
,
,这与条件
矛盾.
所以以上假设不成立.于是
注:题目偏难.