第一学期期终考高二数学试卷
试卷（I）
一、选择题
1、数列
的首项为2，且
（n≥2），则通项公式是：
A、
B、
C、
D、
2、已知数列的通项公式为
，前n项的和为
，则
A、
B、
C、0
D、
3、经过点（5、10）且与原点距离为5的直线的斜率是：
A、
B、
D、或不存在
4、以原点圆心，且截直线
所得弦长为8的圆的方程是：
A、
B、
C、
D、
5、方程
所表示的图形是一个圆，则常数
的值是：
A、2 B、－
6、直线
与直线
平行，则的值是：
A、1 B、－
7、椭圆
上的点P到右焦点距离为
，则P点的横坐标是：
A、
B、
C、
D、
8、给出下列四条不等式：
①
＞
②＞
③ ≥0
④ ＞1
＞ ＞
以上不等式中与不等式
同解的有
A、①③ B、②④ C、③ D、④
9、等差数列
中
，公差
，为前
项的和，要使
…＋
的值最大，则为：
A、7 B、
10、数列满足
，
…＋
（≥2），则
等于：
A、
B、
C、
D、2
二、填空题：
11、直线
关于直线
对称的直线方程是＿＿＿＿＿＿＿＿＿＿
12、不等式
＜
＜8的解集是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
13、与直线
垂直， 且与圆
相切的直线方程是＿＿＿＿＿。
14、数列
的前项和为，设
…＋，则
＝＿＿＿＿＿＿＿
15、等比数列
、
、
，……的通项公式是＿＿＿＿＿＿＿＿＿＿
第一学期期终考高二数学答题卷
试卷（II）
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、 填空题
11、＿＿＿＿＿＿＿＿＿＿＿＿＿＿ 12、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
13、＿＿＿＿＿＿＿＿＿＿＿＿＿＿ 14、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
15、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
三、 解答题
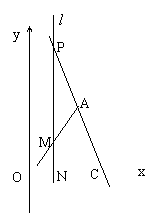
16、如图，已知A（2，3）、C（3，0），不论k取何值，
直线
与直线AB交于定点M，设直线
与
|
时与轴交于点N，
求N点分
所成的比：
17、已知数列的首项为4，且
（≥2），由该逆推式求得
，
， 
，
，试猜想该数列的通项公式，并用数学归纳法加以证明。
18、P为椭圆
上一点，
、
为左右焦点，若
（1）求△
的面积
（2）求P点的坐标
19、过点M（1，4）的直线在两坐标轴上的截距a、b均为正值，当a＋b最小时，求直线的方程。
20、解关于的不等式：
＞
。
答案与评分参考标准
一、选择题（每小题4分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | D | B | B | D | A | D | D | C |
二、填空题（每小题3分）
11、
12、{
或
}
13、
或
14、
15、
三、解答题
16、解：
A是PC的中点 可求得P（1，6）（2分）
直线
即
过定点（1，1）
故M点的坐标是（1，1）（4分）
又N点的纵坐标是0，
故N分
所成比
(8分)
17、解：
，
，，
，（2分）
猜想
（4分）
证明：①当
时，已知
，而
通项公式成立 （5分）
②假设
时，通项公式成立，即
那么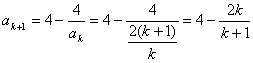
这就是说
的通项公式成立
由①②知通项公式对
成立 （8分）
18、解：a＝5 b＝c＝4 （1分）
（1）设
，则 
（1） （3分）
（2）
（1）2－（2）得
（5分）
（2）设P
，由
得 4
（7分）
将
代入椭圆方程解得
或
或
或
（9分）
19、解：直线的方程为
M（1，4）代入得
（2分） 得
a＞0 b＞0 b－4＞0 （4分）
≥
（8分）
当
即 b＝6 时取等号 a＋b＝9为最小值
a=3
此时直线的方程为
（10分）
20、解：不等式即
＜0
当m＞－1时 △＞0 
有两个不相等的实数根
当m＝－1时 △＝0 当m＜－1 △＜0时无实数根
故：（1）当m＞0时，不等式的解集为
＜＜
（2分）
（2）m＝0时不等式即
＜0 解得
即解集为
（4分）
（3）当－1＜m＜0时 
不等式的解集为
或
（6分）
（4）m＝－1时 不等式即为
故解集为
（8分）
（5）m＜－1时 △＜0 故解集为R （10分）
m＜0