年级:高二 科目:数学
高二(上)期数学(文科)期末试题
一.选择题.(共12小题,每小题5分,共60分)
1.若直线![]() 平行,则
平行,则![]() 的值为( )
的值为( )
A.-1
B
2.设![]() 表示平面,
表示平面,![]() 表示直线,给出下面四个命题:
表示直线,给出下面四个命题:
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
其中正确的是( )
A.(1)(2) B.(1)(2)(3) C.(2)(3)(4) D.(1)(2)(4)
3.双曲线![]() 的离心率
的离心率![]() 的取值范围是( )
的取值范围是( )
A.(-6,6) B.(-12,0) C.(1,3) D.(0,12)
4.点M![]() 内不为圆心的一点,则直线
内不为圆心的一点,则直线![]()
![]()
![]() 与该圆的位置关系是( )
与该圆的位置关系是( )
A.相切 B.相交 C.相离 D.相切或相交
5.已知抛物线的顶点在原点,焦点在![]() 轴上,且抛物线上点
轴上,且抛物线上点![]() 到焦点的距离为4,则
到焦点的距离为4,则![]() 的值等于( )
的值等于( )
A.4
B.
6.在直角坐标系中,点A在圆![]() 上,点B在直线
上,点B在直线![]() 上.则AB最小值为( )
上.则AB最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在正方体ABCD—A1B
A.4条 B.6条 C.8条 D.10条
8.若实数![]() 满足方程
满足方程![]() ,则
,则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.双曲线![]() 的左焦点为F,点P是双曲线左支上位于
的左焦点为F,点P是双曲线左支上位于![]() 轴上方的任一点,则直线PF的斜率的取值范围是( )
轴上方的任一点,则直线PF的斜率的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在△ABC中,∠C=90º,点P是△ABC所在平面外一点,PC=17,P到AC、BC
的距离PE=PF=13.则P到平面ABC的距离是( )
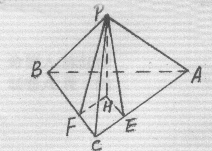
A.7 B.8
C.9 D.10
11.P是抛物线![]() 上一点,P到点A
上一点,P到点A![]() 的距离为
的距离为![]() ,P到直线
,P到直线![]() 的距离为
的距离为![]() ,当
,当![]() 取最小值时,点P的坐标为( )
取最小值时,点P的坐标为( )
A.(0,0)
B.(2,2)
C.(1,![]() )
D.(
)
D.(![]() )
)
12.若椭圆![]() 和双曲线
和双曲线![]() 有共同的焦点F1、F2,且P是两条曲线的一个交点,则△PF
有共同的焦点F1、F2,且P是两条曲线的一个交点,则△PF
A.1
B.![]() C.2
D.4
C.2
D.4
二.填空题.(共4小题,每小题4分,共16分)
13.过点(2,1)且在两条坐标轴上截距相等的直线方程是 .
14.点M与点F(0,-4)距离比它到直线![]() 的距离小于1,则M点的轨迹方程是
.
的距离小于1,则M点的轨迹方程是
.
15.空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,若EF=![]() ,则AD与BC所成的角为 .
,则AD与BC所成的角为 .
16.过点A(3,-1)且被A平分的双曲线![]() 的弦所在直线方程是 .
的弦所在直线方程是 .
三.解答题.(6个小题,17—21每小题12分,22小题14分,共74分)
17.(12分)求以过原点与圆![]() 相切的两直线为渐近线,且以椭圆
相切的两直线为渐近线,且以椭圆![]() +
+![]() 的两焦点为顶点的双曲线方程.
的两焦点为顶点的双曲线方程.
18.(12分)已知曲线![]() .
.
(1)当![]() 为何值时,曲线
为何值时,曲线![]() 表示圆;
表示圆;
(2)若曲线![]() 与直线
与直线![]() 交于M、N两点,且OM⊥ON.(O为坐标原点).求
交于M、N两点,且OM⊥ON.(O为坐标原点).求![]() 的值.
的值.
19.(12分)某木工制作实验柜需要大号木板40块,小号木板100块,已知建材市场出售A、B两种不同型号的木板.经测算知A型木板可同时锯得大号木板2块,小号木板6块,B型木板可同时锯得大号木板1块,小号木板2块.已知A型木板每张40元,B型木板每张16元,问A、B两种木板各买多少张,可使资金最少?并求出最少资金数.
20.(12分)如图,已知平面![]()
![]() ,ABCD为矩形,
,ABCD为矩形,![]() ,PA⊥
,PA⊥![]() ,且PA=AD,M、N、F依次是AB、PC、PD的中点.
,且PA=AD,M、N、F依次是AB、PC、PD的中点.
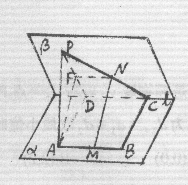
(1)求证:四边形AMNF为平行四边形;
(2)求证:MN⊥AB
(3)求异面直线PA与MN所成角的大小.
21.(12分)已知椭圆C的焦点是![]() 、
、![]() ,点F1到相应的准线的距离为
,点F1到相应的准线的距离为![]() ,过点F2且倾斜角为锐角的直线
,过点F2且倾斜角为锐角的直线![]() 与椭圆C交于A、B两点,使F2B=
与椭圆C交于A、B两点,使F2B=
3F
(1)求椭圆C的方程;
(2)求直线![]() 的方程.
的方程.
22.(14分)如图,已知不垂直于![]() 轴的动直线
轴的动直线![]() 交抛物线
交抛物线![]() 于A、B两点,若A、B两点满足∠AQP=∠BQP,其中Q(-4,0),原点O为PQ的中点.
于A、B两点,若A、B两点满足∠AQP=∠BQP,其中Q(-4,0),原点O为PQ的中点.
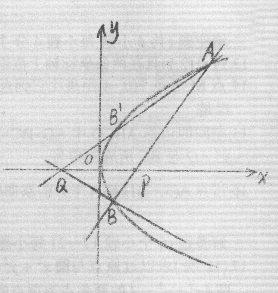
(1)求证:A、P、B三点共线;
(2)当![]() =2时,是否存在垂直于
=2时,是否存在垂直于![]() 的直线
的直线
![]() 被以AP为直径的圆所截得
被以AP为直径的圆所截得
的弦长L为定值?若存在,求出![]() 的方
的方
程;若不存在,说明理由.
高二(上)期数学(文科)期末试题答案
一.选择题.(共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | D | C | C | A | C | D | D | A | B | A |
二.填空题.(共4小题,每小题4分,共16分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
三.解答题.(6个小题,17—21每小题12分,22小题14分,共74分)
17.(12分)
解:设渐近线方程为![]() .则由题意知它们是已知圆
.则由题意知它们是已知圆![]() 的切线
的切线
∴![]() ∴
∴![]() ,即渐近线为
,即渐近线为![]() .
.
易得已知椭圆![]() 的两焦点为
的两焦点为![]() ,它们为所求双曲线的顶点. ∴可设双曲线方程为
,它们为所求双曲线的顶点. ∴可设双曲线方程为![]() .由渐近线方程得
.由渐近线方程得![]() ∴
∴![]()
∴![]() 为所求.
为所求.
18.(12分)
解: (1)![]() .
.
(2)设![]() .则由OM⊥ON得
.则由OM⊥ON得![]()
![]() (*)
(*)
由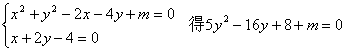
∴![]()
![]() 代入(*) 得:
代入(*) 得:![]()
∴![]()
19.(12分)

解:设买A型木板![]() 张,B型木板
张,B型木板![]() 张,付出资金
张,付出资金![]() 元,则:
元,则:
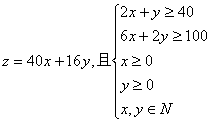
由![]()
由图可知当![]() 时.
时.![]() (元)
(元)
答:买A型木板10张,B型木板20张,付出资金最少为720元.
20.(12分)
![]() 证明: (1)F、N分别为PD、PC的中点
证明: (1)F、N分别为PD、PC的中点![]()
![]()
矩形ABCD,M为AB中点![]()
![]() 四边形AMNF为平行四边形.
四边形AMNF为平行四边形.
![]() (2)由(1)知MN//AF.
(2)由(1)知MN//AF.
![]()
![]()
![]()
![]() AB⊥平面PAD
AB⊥平面PAD ![]() AB⊥AF
AB⊥AF
ABCD是矩形![]() AB⊥AD AFC平面PAD
AB⊥AD AFC平面PAD
![]() AB⊥MN
AB⊥MN
(3)MN//AF![]() ∠PAF是异面直线PA与MN所成的角.
∠PAF是异面直线PA与MN所成的角.

故所求角为45º.
21.(12分)
解: (1)设椭圆C的方程为![]() ,
,
则由已知得:![]() ∴
∴![]() ,
, ![]()
∴![]() 为所求.
为所求.
(2)由椭圆方程知![]()
则![]()
![]()
由![]()
∴![]() ①
①
又F2分![]() 所成的比
所成的比![]()
∴![]() ②
②
由①,②得: ![]()
![]() ∴
∴![]()
∴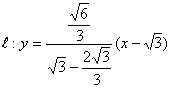 即
即![]()
22.(14分)
证明: (1)设![]() ,则由已知得
,则由已知得![]()
设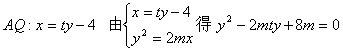
∴![]()
![]() 要证A、P、B三点共线,即证
要证A、P、B三点共线,即证![]()
即![]() 即
即![]()
即![]() 而此式恒成立.
而此式恒成立.
∴A、P、B三点共线.
(2)设![]() ,则由
,则由![]() 及圆心C
及圆心C![]() ,
,
半径![]()
![]() ,假设存在
,假设存在![]() 满足题设条件.
满足题设条件.
则![]() 被⊙C截得的弦长L应有:
被⊙C截得的弦长L应有:
![]()
![]()
要使L为定值,只要![]() ∴
∴![]() 此时L=
此时L=![]() .
.
故存在直线![]() 适合题意.
适合题意.