上学期高二年级数学期中考试2
说明：1、本试卷共6页，共21道题，120分钟完卷。全卷满分为100分。
2、第21题的第（2）问为附加题，该小题的满分为5分，对于试卷总分不足100分的考生加入总分，但最高分不得超过100分。
一、选择题（把正确答案的符号填在试卷的表格中。每小题3分，共36分）
1、不等式
的解集是
A. 
B. 
C. 
D. 
2、设a、b是满足不等式ab<0的实数，那么
A.a+b>a－b B. a+b<a－b C. a－b<a－b D. a-b<a+b
3、 已知c<0,在下列不等式中成立的一个是
A. 
B. 
C. 
D. 
4、已知集合A={x3x－2－x2<0},B={xx－a<0},若
,则a的取值范围是
A.a≤1
B.1<a≤
5.在直角坐标系中，直线
x+3y－2=0的倾斜角为
A.
B. 
C.
D. 
6、三点A (3, 1),B (－2, k), C (8, 11)在同一直线上，则k的值是
A.－6
B.－
7、点(0,5)到直线y=2x的距离是
A.
B.
C. 
D. 
8、若直线
：ax+2y+b=0 (b≠0)与直线
：x+(a－1)y+(a2－1)=0没有公共点，则a等于
A. －1 B
9、已知点(x,y)在直线x+2y=3上移动，则式子
的最小值是
A. 8
B
D. 
10、直线x+
y+2
=0过点（－1，1），且与直线
垂直，那么
A. =1, =0 B.
=0, =
, 
D. 
,
11、A点关于8x+6y=25的对称点恰为原点，则A点的坐标为
A.(2, ) B.
C.(3, 4)
D.(4, 3)
12、已知A(2,－3) 、B(－3,－2),直线
过P(1,1)且与线段AB有交点，设直线的斜率为k,则k的取值范围是
A. k≥
或k<-4 B. -4≤k≤
C.k≥或k≤
D.
≤k≤4
二、填空题（把每小题的答案填在试卷对应题号的横线上。每小题3分共12分）
13、不等式x+1<1的解集为.
14、不等式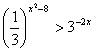
的解集是.
15、经过直线x+3y－4=0与5x+2y+6=0的交点且与直线3x－2y+3=0平行的直线方程是.
16、已知直线与的斜率是方程6x2+x－1=0 的两个根，则与的夹角为.
上学期期中考试
高二年级数学试卷
班级___________学号_____________ 姓名______________ 成绩________________
一、选择题（每小题3分，共36分，把正确答案的符号填在下列表格中）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 小计 |
| 答案 |
二、填空题（每小题3分,共12分. 把每小题的答案填在试卷对应题号的横线上）
13、___________________ 14、___________________________
15、___________________ 16、___________________________
三、解答题（本部分共5道题，满分为52+5分）
17.解下列不等式（2×6=12分）
（1）
（2）
18.（10分）已知△ABC的三个顶点为A(
), B (6, －4)，C(－2，－10 )分别求出BC边上的中线和高所在的直线方程。
19、（10分）m为何值时，关于x的方程
+2(m+1)x+(1－
(1) 有两个异号的实数根. （2）有两个实数根且两根和是非负数。
20．（10分）有一批影碟机（VCD）原销售价为每台800元，在甲、乙两家家电商场均有销售。甲商场用如下方法促销：买一台价格为780元，买两台每台价格为760元，依次类推，每多买一台，则所买各台价格均再减少20元，但每台最低不能低于440元，乙商场一律都按原价的75%销售，某单位需购买一批此影碟机，问去哪家商场购买花费较少？
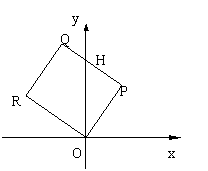
21、在直角坐标系中，设矩形OPQR的顶点按逆时针顺序依次为O(0,0),P(1,t)
Q(1-2t,2+t),R(-2t,2)其中t
(0,+∞),
（1）求矩形OPQR在第一象限部分的面积S(t)。 （10分）
附加题（2）确定函数S(t)的单调区间，并加以证明。（5分）
第一学期期中考试
高二年级数学试题答案及评分标准
一、选择题（每小题3分，共36分，把正确答案的符号填在下列表格中）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 小计 |
| 答案 | B | B | C | A | D | D | B | A | D | B | D | A |
二、填空题（每小题3分共12分）
13、{x｜－2<x<0} 14、{x－2<x<4}
15、2x+3y－3=0 16、450
三、解答题（12+10+10+10+10+5=52+5分）
17、（1）（6分）解：原不等式等价于
……4分
所以原不等式的解集为{xx<－3或－1≤x≤
或x>1}………………6分
(2)（6分） 解：原不等式可化为：
等价于：
……………………………………4分
原等式的解集为{x-< x <-1或1< x < }………………6分
18、（10分）解：由中点坐标公式得BC边的中点D的坐标为 （2，-7）……2分
中线AD所在的方程为：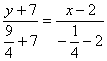
即：3x+9y-11=0…………5分
BC边上的高所在的直线方程为： y
=(x-
) 即：16x+12y-23=0……10分
19、（10分） 解(1)设方程两根为
、
依题意有
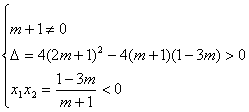…………………………………………4分
解之得 m<－1或m>
…………………………………………………………5分
(2) 有两实数根且和为非负的充要条件是
…………………………8分
即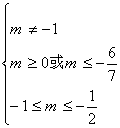
所以： －1<m
……………………10分
20、（10分）设某单位要购买x台影碟机，甲、乙两商场的购货款的差价为y元，则
去甲商场共花费（800－20x）x
据题意 800－20x≥440…………………………2分
去乙商场共花费600, x∈N
∴
=
…………………………………………7分
得：
(1)当１≤x<10时(x∈N)， y>0去乙商场花费少
(2)当x=10时(x∈N)， y=0去甲、乙商场花费一样………………………………9分
(3)当10<x≤18时(x∈N)，y<0去甲商场花费少
故 若买少于10台，去乙商场花费较少，若买10台，去甲乙商场花费一样；若买超过10台去甲商场花费较少。……………………………………10分
21、(10分+5分)解：（I）当1－2 t>0 即 0<t<时，
如图点Q在第一象限时，此时S(t)为四边形OPQK的面积，
直线QR的方程为y－2=t(x+2t)…………………………2分
令x=0，得 y=2t2+2 ,点K的坐标为（0，2t2+2）
=
=
………………………………5分
当1－2t≤0即t≥时，如图，点Q在y轴或第二象限，S(t)为△OPH的面积
直线PQ 的方程为
点H的坐标为（0，
）
=
…………7分
∴ 
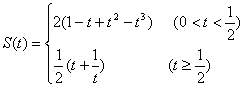……10分
(2)当0<t<时，对于任何0<t1<t2<有s(t1)－s(t2)=2(t2－t1)[1－(t1+t2)+(
)]>0
即s(t1)
> s(t2),所以s(t)在区间（0，）内是减函数。……………………1分
当t≥时，对于任何≤t1≤t2,有s(t1)－s(t2)= (t1－t2)（1－
）…………2分
所以当≤t1≤t2时, s(t1) > s(t2),若1≤t1≤t2时s(t1) < s(t2)
所以s(t)在区间[，1]内是减函数，在区间
内是增函数，………………3分
由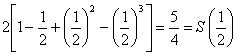
以及上面的证明过程可得，
对于0<t1<≤t2<1, S(t2)<
≤S(t1),
…4分
于是S(t)的单调区间分别为
及且S(t)在内是减函数，在内是增函数。
………………………………………………5分