上学期高二数学期末测试题(D)

上学期高二数学期末测试题(D)

班次　　　  学号　　　　  姓名　　　　　　

一、 选择题：（每小题5分，共50分）

1.如果的平均数为3，那么、、、

、、的平均数是（　　）

A.0　　　　  B.3　　　　C.6　　　　D.12

2.已知、是异面直线，下列命题中的真命题的个数为（　　）

①过可以作与垂直的平面；②过可以作与平行的平面；

③过空间任意一点可以作与、都平行的平面；

④存在平面α、β，使α， β，且α⊥β.

A. 0　　　　　 　B. 1　　　　　　　 C. 2　　　　　　  D. 3

3.已知点B是在坐标平面上的射影，则 =（　　 ）

A.25　　　　　  B.16　　　　　　  C. 5　　　　　　  D. 3

4. 展开式中不含的项的系数和为（　　 ）

A.　　　　　  B.16　　　　　　  C. 5　　　　　　　D. 3

5.要从10名女生与5名男生中选取6名学生组成6名课外兴趣味小组，如果按性别

分层随机抽样，试问组成课外兴趣小组的概率是（　　）

A．　　　 B．　　　　 C．　　　　 D．

6. 在地球北纬60°圈上有A、B两点，它们的经度相差180°，则A、B两点沿纬度

圈的弧长与A、B两点间的球面距离之比为（　　 ）

A. 　　　　B. 　　　　　　　C. 　　　　　D.

7. =（　　 ）

A. 1　　　　　  B. 4　　　　　　　 C. 6　　　　　　  D. 不存在

8. 有一排7只发光二极管，每只二极管点亮时可发出红光或绿光，若每次恰有3只

二极管点亮，但相邻的两只二级管不能同时点亮，根据这三只点亮的二极管的不

同位置或不同颜色来表示不同的信息，则这排二极管能表示的信息种数共

有（　　 ）

A．10　　 　　B．48 　　　　C．60　　　　　D．80

9. 已知,假设存在函数

　则是（　　　）

A.偶函数且有最大值　　　　　　　　　B.奇函数且有最大值　

C. 奇函数且有最小值　　　　　　　　　D.偶函数且有最小值

10.如下图，有一个三角形的遮阴棚△ABC，AC=3m，BC=4m，AB=5m，A、B是安置在地面上南北方向的两个定点，由正西上方的太阳（用点O表示）射出的光线OCE与地面成30°的角，△ABE为遮阴棚产生的阴影，当遮阴棚与地面搭成60°的二面角时，该遮阴棚所遮阴影△ABE的面积是（　　 ）

A. 48m² 　 B. 24m²C. 12m²　 　 D. 3m²

二、 填空题：（每小题5分，共25分）

11.观察下表:　 1

2　　3　　4

3　　4　　5　　6　　7

4　　5　　6　　7　　8　　9　 10

…　 …

设第n行的各数之和为s_n，则=　　　　 .

12. 三个外宾参加会议,前排9个座位中,要求相邻二外宾间至少二个座位留给本地代表,则外宾不同坐法种数是_________.(用数字作答)

13. 随机变量的概率密度，

则=__________

14. 抛一枚均匀硬币，正、反每面出现的概率都是，反复这样的投掷.数列定义如下：a_n=　txjy若S_n=a₁+a₂+…+a_n(n∈N⁺)，则事件“S₈=2” 的概率为_________，事件“S₂≠0，且S₈=2”的概率为_______________.

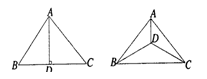15. 如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：

①；②∠BAC=60°；

③三棱锥D—ABC的正三棱锥；

④平面ADC的法向量和平面ABC的法向量互相垂直.

其中正确结论的序号是　　　　　  .

三、 解答题：（本大题共75分，分别为124，13，14分）

16．（本小题满分12分）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内，求：

(1)只有一个盒子空着，共有多少种投放方法？

(2)没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

(3)每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？

17．（本小题满分12分）已知展开式中的倒数第三项的系数为45，

求：⑴含的项；⑵系数最大的项．

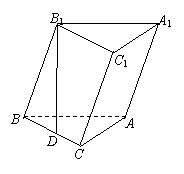
18．（本小题满分12分）已知斜三棱柱ABC—A₁B₁C₁的底面是直角三角形，∠C=90°，

侧棱与底面所成的角为α　(0°＜α＜90°＝，点在底面上的射影落在上．

(1)　 求证：AC⊥平面BB₁C₁C；(2)若AB₁⊥BC₁，D为BC的中点，求α ；

(3)若α = arccos ，且AC=BC=AA₁时，

求二面角C₁—AB—C的大小．

19．（本小题满分12分）甲乙两个实力相当的乒乓球运动员进行比赛，比赛规则是每赛一场，胜者记一分，先得5分者为胜，奖金总额为10万元，按两人的得分比例进行分配，例如甲得5分，乙得3分；则甲得奖金的八分之五，即6.25万元。当比赛进行到4:3时，由于客观原因(不是任何一方运动员造成的原因)而终止比赛，奖金如何分配呢?得4分的甲主张按4:3的比例分配,乙不同意，主张平均分奖金;理由是如果继续比赛的话，乙还有获胜的机会。你认为如何分配才算合理?

20. （本小题满分13分）据统计，某同学数学考试得120分以上的概率为

⑴设为该同学2007年上期6次考试中得分在120分以上的次数，求的分布列。

⑵设为该同学2007年上期6次考试中首次得分在120分以上的经过的考试次数，

求的分布列。

⑶求该同学2007年上期6次考试中至少一次在120分以上的概率。

21. （本小题满分14分）已知

⑴已知数列极限存在且大于零，求（将A用a表示）；

⑵设

⑶若都成立，求a的取值范围.

参考答案：
1~10 ACCAA ACDAC

11. 4　12. 60　13. 　14.   15.②③

16．解:(1)C₅²A_­5⁴=1200（种）　　　　　　　　  ……4分

(2)A₅⁵-1=119（种）　　　　　　　　　　　 ……8分

(3)不满足的情形：第一类，恰有一球相同的放法：　C₅¹×9=45

第二类，五个球的编号与盒子编号全不同的放法：

∴ 满足条件的放法数为：　  A₅⁵-45-44=31（种）　　　 ……12分

17．解：⑴由题设知

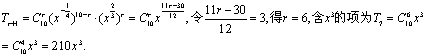　 ⑵系数最大的项为中间项，即

18．解 (1)∵　B₁D⊥平面ABC，　AC平面ABC，

∴　　B₁D⊥AC， 又AC⊥BC，  BC∩B₁D=D．

　　　　 ∴　AC⊥平面BB₁C₁C．

₍₂₎ ∵ AC⊥平面BB₁C₁C ，AB₁⊥BC₁ ，由三垂线定理可知，

　　　　　 　B₁C⊥BC₁．

　　　　 ∴　平行四边形BB₁C₁C为菱形，此时，BC=BB₁．

　　　　 又∵ B₁D⊥BC，D为BC中点，B₁C= B₁B，∴△BB₁C为正三角形，

　　　　 ∴　∠B₁BC= 60°．

(3)过C₁作C₁E⊥BC于E，则C₁E⊥平面ABC．

过E作EF⊥AB于F，C₁F，由三垂线定理，得C₁F⊥AB．

∴∠C₁FE是所求二面角C₁—AB—C的平面角．

设AC=BC=AA₁=a，

在Rt△CC₁E中，由∠C₁BE=α=，C₁E=．

在Rt△BEF中，∠EBF=45°，EF=BE=a．

∴∠C₁FE=45°，故所求的二面角C₁—AB—C为45°．

解法二：(1)同解法一  

(2)要使AB₁⊥BC₁，D是BC的中点，即=0，=，

∴， =0，∴．

∴，故△BB₁C为正三角形，∠B₁BC=60°；

∵　B₁D⊥平面ABC，且D落在BC上，

　　　 ∴ ∠B₁BC即为侧棱与底面所成的角．

　　　故当α=60°时，AB₁⊥BC₁，且D为BC中点．

(3)以C为原点，CA为x轴，CB为y轴，经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系，则A(a，0，0)，B(0，a，0)，C(0，-，a)，

平面ABC的法向量n₁=(0，0，1)，设平面ABC₁的法向量n₂=(x，y，z)．

由n₂=0，及n₂=0，得

　 ∴n₂=(，，1)．

cos＜n₁， n₂＞= = ，

故n₁ ， n₂所成的角为45°，即所求的二面角为45°

19.由于实力相当,故获胜的概率均为0.5,一个合理的方案是按其可能的比赛

结果的平均数（即期望）分配:

若继续比赛可分为三种情形5:3,5:4,4:5，则甲得:

故甲得5.625万元，乙得4.375万元.

20. （1）将该同学2007年上期6次考试中的每次考试看做一次试验，则得分在120分以上的概率为，且每次实验结果是相互独立的。

故，以此求的分布列

所以的分布列为

（2）由于表示该同学2007年上期6次考试中首次得分在120分以上经过的年数，显然是随机变量，其取值为0，1，2，3，4，5，

其中表示前次没有得到120分以上，但在第次得到了120分以上的情况，故各概率应按独立事件同时发生计算。

而表示这6次该同学没有得到120分以上的情况，

故其概率为,因此的分布列为：

	0	1	2	3	4	5	6

（3）该同学2007年上期6次考试中至少一次得分在120分以上的事件为

所以

21. （I）由

（II）

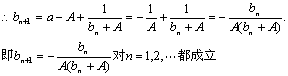
（III）

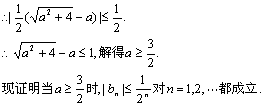
　　　　 （i）当n=1时结论成立（已验证）.

　　　　 （ii）假设当

　　　　

　　　　 故只须证明

　　　　

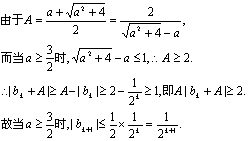
　　　　 即n=k+1时结论成立.

　　　　 根据（i）和（ii）可知结论对一切正整数都成立.

　　　　 故