上学期高二数学期中试题
第一卷(共60分)
一、 选择题(本大题共12小题,每小题5分,共60分)
1. 如果![]() <
<![]() 且
且![]() <
<![]() ,则直线
,则直线![]() 不通过
(
)
不通过
(
)
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.过点M(-4,3)和N(-2,1)的直线方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.圆![]() 对称的圆的方程是( )
对称的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.方程![]() 和
和![]() 在同一坐标系中的图形可能是
(
)
在同一坐标系中的图形可能是
(
)
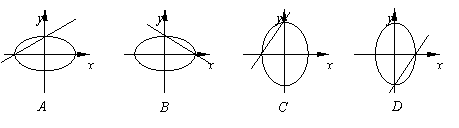
5.抛物线![]() 的焦点坐标为
( )
的焦点坐标为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.直线![]() :
:![]() ,
,![]() :
:![]() ,如果
,如果![]() ∥
∥![]() ,则
,则![]() 的值为
(
)
的值为
(
)
A. ![]() B.
B.
![]() C.
C.
![]() 或
或![]() D.
D. ![]() 或
或![]()
7.直线![]() 绕原点按逆时针旋转30°后所得直线与圆
绕原点按逆时针旋转30°后所得直线与圆![]() 的位置关系是
( )
的位置关系是
( )
A. 直线过圆心 B. 直线与圆相交,但不过圆心
C. 直线与圆相切 D. 直线与圆没有公共点
8.与椭圆![]() 共焦点,且两准线间的距离为
共焦点,且两准线间的距离为![]() 的双曲线方程为 ( )
的双曲线方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9. 若直线![]() 为在
为在![]() 轴上截距为3,在
轴上截距为3,在![]() 轴上截距为
轴上截距为![]() 的直线,直线
的直线,直线![]() 的程为
的程为![]() ,直线
,直线![]() 到直线
到直线![]() 的角为45°,则
的角为45°,则![]() 的值为 ( )
的值为 ( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]() 或3
或3
10.两定点A(-2,-1),B(2,-1),动点P在抛物线![]() 上移动,则△PAB重心G的轨迹方程是 ( )
上移动,则△PAB重心G的轨迹方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.直线![]() =4得的劣弧所对的圆心角(
)
=4得的劣弧所对的圆心角(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.定长为![]() 的线段AB的端点在双曲线
的线段AB的端点在双曲线![]() 的右支上,则AB中点M的横坐标的最小值为 ( )
的右支上,则AB中点M的横坐标的最小值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
![]() 第二卷(共90分)
第二卷(共90分)
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
二、 填空题(本大题共4小题,每小题4分,共16分)
13.直线![]() 恒过一定点,则这一定点是 .
恒过一定点,则这一定点是 .
14.设椭圆![]() 的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦长等于F1到l1的距离,则椭圆的离心率为
.
的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦长等于F1到l1的距离,则椭圆的离心率为
.
15.F1,F2是双曲线![]() 的两个焦点,P是双曲线上的一点,已知PF1,PF2,F1F2依次成等差数列,且公差大于0,则∠F1PF2= .
的两个焦点,P是双曲线上的一点,已知PF1,PF2,F1F2依次成等差数列,且公差大于0,则∠F1PF2= .
16. 圆心在抛物线y2=2x上,且与x轴和该抛物线的准线都相切的一个圆的方程是 .(写一个即可)
三、解答题(本大题共6小题,共74分.写出必要的解题步骤.)
17.(12分)已知圆![]() 过点
过点![]() 、
、![]() ,且圆心在直线
,且圆心在直线![]() 上,求圆
上,求圆![]() 的方程.
的方程.
18.(12分)直线![]() 经过两直线
经过两直线![]() 和
和![]() 的交点,且点
的交点,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
19.(12分)双曲线的中心在坐标原点,对称轴为坐标轴,两个焦点为F1、F2,一条渐进线方程为![]() ,且经过点
,且经过点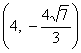 ,又点P在双曲线上.若P F1
,又点P在双曲线上.若P F1![]() P F2,求点P到x轴的距离.
P F2,求点P到x轴的距离.
![]() 20.(12分)某工厂库存A、B、C三种原料,可用来生产Z、Y两种产品,市场调查显示可获利润等各数据如下表:
20.(12分)某工厂库存A、B、C三种原料,可用来生产Z、Y两种产品,市场调查显示可获利润等各数据如下表:
|
| A | B | C | 每件产品利润(元) |
| 库存量(件) | 100 | 125 | 156 |
|
| Z(每件用料) | 1 | 2 | 3 | 2000 |
| Y(每件用料) | 4 | 3 | 1 | 1000 |
问:若市场情况如图所示,怎样安排生产能获得最大利润?
 |
21.(12分)已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,准线方程为
轴上,准线方程为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 交于A、B两点,
交于A、B两点,![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 过点
过点![]() 和抛物线
和抛物线![]() 的焦点
的焦点![]() ,且直线
,且直线![]() 的倾斜角为
的倾斜角为![]() ,求直线
,求直线![]() 的方程.
的方程.
![]() 22(14分)设
22(14分)设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() :
:![]() 的左、右两个焦点.
的左、右两个焦点.
(1)若椭圆![]() 上的点
上的点![]() 到
到![]() 、
、![]() 两点距离之和等于4,写出椭圆
两点距离之和等于4,写出椭圆![]() 的方程和焦点坐标;
的方程和焦点坐标;
(2)设点![]() 是(1)中所得椭圆
是(1)中所得椭圆![]() 上的动点,求线段
上的动点,求线段![]() 的中点的轨迹方程;
的中点的轨迹方程;
(3)已知椭圆具有性质:若![]() 是椭圆
是椭圆![]() :
:![]() 上关于原点对称的两个点,点
上关于原点对称的两个点,点![]() 是椭圆上任意一点,当直线
是椭圆上任意一点,当直线![]() 的斜率都存在,并记为
的斜率都存在,并记为![]() ,那么
,那么![]() 之积是与点
之积是与点![]() 位置无关的定值.试对双曲线
位置无关的定值.试对双曲线![]() :
:![]() 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.