圆锥曲线2椭圆

圆锥曲线2 椭圆

一、选择题.

1、已知椭圆上一点P到准线距离与它到相应于这条准线的焦点的距离的比为　　(　　)

(A) (B) (C) (D)

2、若直线y = x＋t与椭圆相交于A,B两点,当t变化时,AB的最大值为

 (　　)

(A)2  (B) (C) (D)

3、F₁,F₂是椭圆的两个焦点,过F₂作倾斜角为的弦AB,则F₁AB的面积为　　　　　　　　　　　　　　　　　　　　　　　　　　　 　(　　)

(A) (B) (C) (D)

4、过点A(a,0)作椭圆的弦,弦中点的轨迹仍是椭圆,若原椭圆和轨迹椭圆的离心率分别为e和,则e,的关系是(　　)

(A) (B)(C)(D)不能确定

5、过椭圆4x²＋2y² = 1的一个焦点F₁的直线与椭圆相交于A,B两点,则A,B与椭圆的另一个焦点F₂构成的ABF₂的周长等于　　　　　　　　　　　  (　　)

(A)2  (B)4　(C)8　 (D)2

6、椭圆上对两焦点张角为90⁰的点可能有　　(　　)

(A)　 4个　　　　　　　 (B)2个或4个

（C)0个或2个或4个　　(D)还有其他情况

7、P为椭圆上的动点,作PDx轴,D是垂足,则PD中点轨迹方程是(　　)

(A)　　(B)　　(C)　　(D)

8、已知椭圆,P为椭圆上一点,且,则点P的坐标为　(　　)

(A)(2,3)　　　(B)(

 (C)(　　(D)(4,

9、L为定直线,F为不在L上的定点,以F为焦点,L为准线的椭圆可画　　　 (　　)

(A)1个　　　　  (B)2个　　　　  (C)1个或2个　　　　 (D)无穷多个

10、已知椭圆

的焦点在y轴上,则的取值范围是(　　)

(A) (B)

 (C) (D)

11、k为何值时,直线y = kx＋2和椭圆2x²＋3y² = 6相交　　　　　　  (　　)

(A)

 (B)

(C)

 (D)

12、F(c,0)为椭圆的右焦点,F与椭圆上的点的距离最大值为M,最小值为m,则椭圆上与F点距离等于的点是(　)

(A)(C, (B)(－C,

 (C)(0, (D)不存在

13、长轴长20,离心率为0.6的椭圆的标准方程是(　　)

(A)

 (B)

(C)

 (D)

14、已知圆内的一个定点作圆C与已知圆相切,则圆C的圆心轨迹是　　　 (　　)

(A)圆　　　　 (B)椭圆　　

(C)圆或椭圆　　　　  (D)线段

15、椭圆=1上的一点M到一条准线的距离与M到相应焦点的距离之比为 (　)

 (A)

二、

1、(1)离心率=，一条准线方程为x=的椭圆的标准方程为________________；

(2)短轴端点与焦点间的距离等于5，一条准线的方程是y=，且中心在原点的椭圆的方程为___________________。

2、(1)椭圆=1上有一点P到右焦点的距离为1，则P的坐标为_______；

(2)AB是过椭圆的左焦点的弦，且两端点A、B的横坐标之和为-7，则=____________。

3、椭圆的中心在原点，一个焦点为F（0，6），中心到准线的距离为10，则椭圆方程为＿＿。

4、椭圆的中心在原点，短轴端点到焦点的距离是6，一条准线方程是y=9，则椭圆方程为_____________.

5、设P是椭圆在第一象限部分上的点，A、B是椭圆与x轴、y轴正半轴的交点，O为坐标原点，若四边形OAPB面积最大，则点P的坐标是___________

6、设椭圆的左焦点是原点，左准线为x=－p(p＞0)，则椭圆短轴端点的轨迹方程是______

7、在椭圆中，内接△ABC的一边BC与长轴重合，A是椭圆上的动点，△ABC的重心轨迹方程是________________

8、已知动点B(x,y)在椭圆x²＋2y²=98上，若定点A(0，5)与点B的距离最大时，点B的坐标为________，AB的最大值为________________。

9、椭圆的短轴长、焦距、长轴长成等差数列，则这椭圆的离心率为____________

10、椭圆上横坐标为3的点P到两焦点的距离分别为6.5和3.5，那么中心在原点、焦点在x轴上的椭圆方程为________________

三、

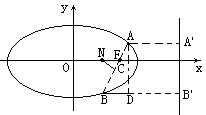
1、已知椭圆,过焦点不垂直于x轴的弦交椭圆于A、B两点,AB的垂直平分线交x轴于N,求NF ： AB的值(图).

2、已知椭圆的中心在原点,焦点在x轴上,椭圆和直线l：x＋2y－2 = 0交于A,B两点,且AB = ,线段AB中点为(1,),求椭圆的方程。

3、椭圆,一弦AB中点的横坐标为定值m(AB不与x轴垂直),求证AB的垂直平分线必过定点,并求出这个定点的坐标。

4、椭圆,直线Ax＋By = 1,直线交椭圆于点P,Q,O为原点,已知OPOQ,求A,B,a,b应满足的关系式.

5、直线l过点P（－1，0），倾斜角为，设（1）；（2），分别求l在椭圆x²＋2y² = 4上截得的弦长。