夹角距离和简单的多面体测验题
姓名： 班别： 学号： 成绩：
一.选择题
1．集合A＝{正方体}，B＝{长方体}，C＝{正四棱柱}，则A、B、C之间的关系为
( )
A.AÌBÌC B.AÌCÌB C.CÌAÌB D.BÌAÌC
2．已知MN是异面直线a与b的公垂线，直线c⊥a,c⊥b,则c与MN的位置关系是 ( )
A．平行 B．垂直 C．平行或重合 D．不确定
3.平面
截一个三棱锥,如果截面是梯形,那么平面必定和这个三棱锥的( )
(A)某条棱平行 (B)某个侧面或底面平行
(C)某条棱垂直 (D)某个侧面或底面垂直翰林汇
4．四棱柱作为平行六面体的充分不必要条件是 （ ）
(A)底面是矩形 (B)侧面是平行四边形
(C)一个侧面是矩形 (D)两个相邻侧面是矩形
5．长方体ABCD－A'B'C'D'中，E、F、G分别是AB、BC、BB'上的点，则△EFG的形状是
( )
A.等边三角形 B.直角三角形
C.锐角三角形
D.钝角三角形
6、如果三棱锥S－ABC的底面是不等边三角形，侧面与底面所成的二面角相等，且顶点S在底面的射影O在△ABC内，那么O是△ABC的
( )
(A)垂心 (B)重心 (C)外心 (D)内心翰林汇
7．在一个45°的二面角的一个面内有一条直线与二面角的棱成45°，则此直线与二面角的另一个面所成的角为 ( )
A．30° B．45° C．60° D．90°
8．三棱锥成为正三棱锥的充分而非必要条件是 （ ）
(A)三棱锥的高通过底面三角形的外心
(B)各个侧面是全等的等腰三角形
(C)四个面都是正三角形
(D)底面是正三角形，且棱锥的高通过底面三角形中心
9．长方体A1B1C1D1-ABCD的底边BC的中点是M，则过A,M,D1的截面是 （ ）
(A)三角形 (B)四边形 (C)五边形 (D)六边形
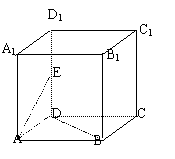10.如图正方体
,
是
的中点,则异面直线
与
所成角的余弦值等于 (
)
A.
B.
C.
D.
11. 已知PA、PB、PC两两垂直,空间M一点到PA、PB、PC的距离分别为4,6,12则MP的长为 ( )
(A)6
(B)6
(C)7 (D)7翰林汇
12、三棱锥D－ABC的三个侧面与底面全等，且AB=AC=，BC=2，则以BC为棱，以面BDC与面BCA为面的二面角大小是
( )
(A)300 (B)450 (C)600 (D)900
二.填空题翰林汇
13.长方体的六个面的面积和为11，所有棱长之和为24，则这个长方体的一条对角线长为 翰林汇
14．若正四棱锥的所有棱长都是a，那么它的底面中心到侧棱之距为
15．正四棱锥的侧棱与底面所成角为450，那么侧面与底面所成的二面角的余弦值是 。
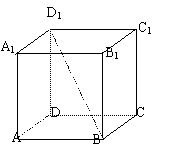16.如图在正方体中,与直线
垂直的一个平面可以是 .
17．棱锥被一平行于底面的平面所截，若截面面积与底面积之比是1：2，则这个截面把一条侧棱分成的上下两段之比是 。
18．下列四个命题：
（1）底面是三角形，其余各面是全等的等腰三角形的棱锥是正棱锥
（2）底面是正三角形，侧面和底面所在平面所成的锐二面角相等的棱锥是正三棱锥
（3）有两个对角面是矩形的平行六面体是直四棱锥
（4）一个正棱锥的各个侧面都是正三角形,则它只能是正三棱锥和正四棱锥
其中真命题的 。
三．解答题
19.如图，已知正三棱柱ABC-A1B1C1 的棱长为1， BM=3MC,在直线CC1 上求一点N,使MN⊥AB1 。
20.已知斜三棱柱ABC-A
BC的侧面A1ACC1 与底面ABC垂直，
，BC=2，AC=
,且
(1) 求侧棱AA1与底面ABC所成的角的大小
(2) 求侧面A1ABB1与底面ABC所成的二面角的大小
(3) 求顶点C到侧面A1ABB1的距离。
21．
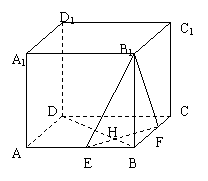如图所示，在棱长为a的正方体ABCD-A1B1C1D1中，E、F分别为棱AB和BC的中点，EF与BD交于H，
（1）求二面角B1-EF-B的大小；
（2）试在棱 BB1上找一点M，使D1M⊥平面B1EF，并证明你的结论；
（3）求点D1到平面B1EF的距离；