简单的线性规划练习

简单的线性规划练习

一、选择题（每小题四个选项中，只有一项符合题目要求）

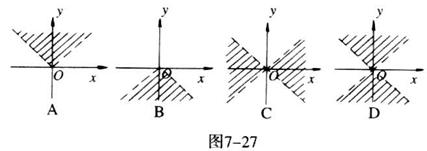
1．如图7-27，表示的平面区域是（　）

2．已知点（3，1）和（-4，6）在直线3x-2y+a=0的两侧，则a的取值范围是（　）

A．a<-7或a>24

B．a=7或a=24

C．-7<a<24

D．-24<a<7

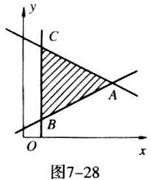
3．给出平面区域如图7-28所示，其中A（5，3），B（1，1），C（1，5），若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个，则a的值是（　）

A．

B．

C．2

D．

二、填空题

4．不等式x-2+y-2≤2表示的平面区域的面积为____________。

5．z=3x+2y，x、y满足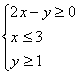，在直线x=3上找出三个整点可行解为__________。

6．给出下面的线性规划问题：求z=3x+5y的最大值和最小值，使x、y满足约束条件，欲使目标函数z只有最小值而无最大值，请你设计一种改变约束条件的办法（仍由三个不等式构成，且只能改变其中一个不等式），那么结果是__________。

三、解答题

7．已知x、y满足不等式组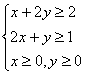，求z=3x+y的最小值。

8．下表给出X、Y、Z三种食品的维生素含量及其成本

	X	Y	Z
维生素A/单位/千克	400	500	300
维生素B/单位/千克	700	100	300
成本/（元/千克）	6	4	3

现欲将三种食物混合成100千克的混合食品，要求至少含35000单位维生素A，40000单位维生素B，采用何种配比成本最小？

9．运输公司接受了向抗洪抢险地段每天至少运输180吨支援物资的任务。该公司有8辆载重6吨的A型卡车与4辆载重量10吨的B型卡车，有10名驾驶员。A型卡车每天可往返4次，B型卡车每天可往返3次。每辆卡车每天往返成本A型为320元，B型为504元。问怎样调配车辆，使公司成本最低？

10．某人上午7时，乘摩托艇以匀速v海里/小时（4≤v≤20）的速度从A港出发到距50海里的B港去，然后乘汽车以匀速w千米/小时（30≤w≤100）的速度自B港到距300千米的C市去，应该在同一天下午4至9点到达C市。

设汽车、摩托艇所需要的时间分别为x、y小时

（1）用图表示满足上述条件的x、y的范围；

（2）如果已知所需要的经费p=100+3(5-x)+(8-y)（元），那么v、w分别是多少时走得最经济？此时需花费多少元？

11．某公司计划在今年同时出售电脑和智能空调这两种商品。由于这两种商品的市场需求量非常大，有多少就能销多少，因此该公司要根据实际情况（如资金、劳动力）确定产品的月供应量，以使得总利润达到最大。已知对这两种产品有直接限制的因素是资金和劳动力，通过调查，得到关于这两种产品有关数据如下

资金	单位产品所需资金/百万		月资金供应量
	电脑	空调
成本	30	10	300
劳动力	5	10	110
单位利润	6	8	—

问怎样确定两种货物的月供应量，才能使总利润达到最大，最大利润是多少？

答案与提示

一、1．D

2．C

3．B

二、4．8

5．（3，1），（3，2），（3，6）

6．把y≤x+1中的等号去掉，也可把6x+3y≤15中的等号去掉

三、7．当x=0，y=1时，

8．最优解为x=30，y=10，从而z=60， （元）

9．每天调用A型卡车5辆，B型车2辆时，公司总成本最低，为2608元

10．（1）略。（2）v=12.5，w=30，p的最小值为89元

11．月供应电脑4台，空调9台时，该店可获得最大利润，最大利润为9600万元