第21课时 空间两直线的位置关系（1）
一、选择题
1．空间三条直线a、b、c，其中a∥b，c和a相交，c与b的位置关系一定是 （ ）
A．相交 B．异面 C．异面或相交 D．异面或相交或平行
2．在正方形ABCD-A
BCD中,与对角线AC异面棱有 （ ）
A．3条 B．4条 C．6条 D．8条
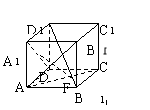3．如图，正方体ABCD-ABCD中，EF是异面直线AC和AD的公垂线，则EF和BD关系是
（ ）
A．相交不垂直 B．相交垂直
C．异面直线 D．互相平行
二、填空题
4．“a、b为异面直线”是指：①a∩b=
，但a不平行于b； ②a
平面α，b平面β，且a∩b=； ③a平面α，b平面β，且α∩β=； ④a平面α，b
平面α；⑤不存在平面α，能使a平面α且b平面α成立．上述结论中正确序号指
．
5．把两条异面直线看成“一对”，那么六棱锥棱所在的12条直线中，异面直线共有 对．
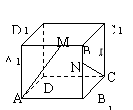6．如图所示，在空间四边形ABCD中，E、F、G、H依次是AB、BC、CD、DA中点，若AC⊥BD，AC=6，BD=4，则EG=
．
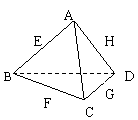
7．在棱长为1的正方体ABCD-ABCD中，M和N分别是AB和B B中点，那么直线AM和CN成角余弦值是
．
8．对于四面体ABCD，给出下列四个命题：①若AB=AC，BD=CD则BC⊥AD；②若AB=CD，AC=BD则BC⊥AD；③若AB⊥AC，BD⊥CD则BC⊥AD；④若AB⊥CD， BD⊥AC则BC⊥AD；其中真命题序号是 ．
三、解答题
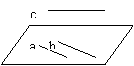9．如图所示，已知直线a、b、c及平面α，c∥平面α，a平面α，b平面α，且a∥b，a、c异面直线，求证b和c是异面直线．
反思回顾
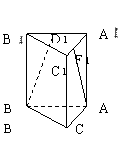10．如图所示，ABC-ABC是直三棱柱，∠BCA=90°，点D、F分别是AB和AC中点，若BC=CA=CC，求BD和AF成角余弦值．
11．已知正方体ABCD-ABCD中，M、N分别是AB和BC中点．
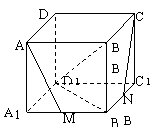（1）AM和CN是否是异面直线？
说明理由．
（2）DB和CC是否是异面直线？
说明理由．
（3）求CN和DB成角．
四、思考题
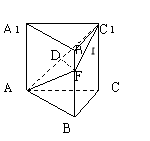12．如图正三棱柱ABC -ABC各棱长均为a，D是AC中点，F为BB上一点，当
为多少时，FD是异面直线AC和BB公垂线段，并证明你的结论．
反思回顾
第22课时 空间两直线的位置关系（2）
一、选择题
1．两条异面直线在同一平面内射影是 （ ）
A．两条相交直线 B．两条平行直线
C．两条相交或平行直线 D．以上情况均不同
2．有一正方提纸盒展开如图，在原正方体纸盒中有如下结论：①AB⊥EF②AB和CM成60°③EF和MN为异面直线④MN∥CD，其中正确序号是
（ ）
A．①②
B．③④
C．②③
D．①③
3．若a、b为异面直线，A、B在直线a上，点C、D在直线b上，且AC=AD，BC=BD，则直线a、b成角为 （ ）
A．90° B．60° C．45° D．30°
二、填空题
4．有以下命题：①和两条异面直线都相交两直线是异面直线；②若两直线都和第三条直线垂直，那么两直线平行；③若两条直线都和第三条直线平行，那么两条直线平行；④和两条异面直线都垂直的直线叫两异面直线的公垂线；其中不正确序号是 ．
5．在正三角形ABC中，D、E、F分别是各边中点，G、H、I、J分别是AF、AD、BE、DE中点，把△ABC沿DE、EF、DF拆成三棱锥后，GH和JI成角度数是
．
6．在正方体ABCD-ABCD中，面对角线AC、BC、BD和AD所在直线成60°角有
（注：把你认为符合条件都填上）．
7．在三棱锥A-BCD中，AC和BD成角60°，且AC=BD，E、F分别是AB、CD中点，则EF和AC成角是 ．
8．如上图，在棱长为1的正方体ABCD-ABCD中，O为正方形ABCD中心，E、F分别是AB、BC中点，则异面直线EF和CO的距离为 ．
三、解答题
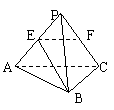9．如图，已知P为△ABC所在平面外一点，E为PA中点，F为PC中点，BE⊥AC，PC⊥AC．
（1）求证：EF是BE、PC公垂线．
（2）若PA=a，PC=b，求异面直线BE、PC间距离．
反思回顾
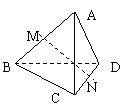10．如图，在三棱锥A-BCD中，AC=BD=a，对棱AC与BD成60°角，M、N分别是AB、CD中点，求线段MN长．
11．在长方体ABCD-ABCD中，AB=BC=2，AA=1，E、H分别是AB和BB中点．
（1）EH和AD成角．
（2）AC和BC成角．
四、思考题
12．如图所示，在二面角α-l-β中，A、B
面α，C、Dl，ABCD是矩形，Pβ，PA⊥面α且PA=AD，M、N依次为AB、PC中点．
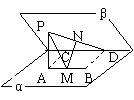（1）求证MN是异面直线AB和PC公垂线．
（2）求异面直线PA和MN成角．
反思回顾
第23课时 直线与平面平行
一、选择题
1．如果直线a∥平面β，那么 （ ）
A．平面β内不存在与a垂直的直线
B．平面β内有且只有一条直线与a垂直
C．平面β内有且只有一条直线与a平行
D．平面β内有无数条直线与a不平行
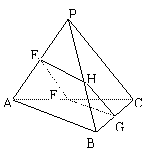2．正三棱锥P_ABC的底面边长为1，E、F、G、H分别是PA、AC、BC、PB中点，四边EFGH面积记为
，那么值域是 （ ）
A．{
}
B．（0，+∞）
C．（
，+∞） D．（
，+∞）
3．已知直线a、b、c和面α，下列条件能使a∥b成立的是 （ ）
A．a∥面α且b∥面α B．a⊥c且b⊥c
C．a∥c且b∥c D．a、b与面α成角相等
二、填空题
4．A、B到平面α距离分别为4cm和6cm，那么线段AB中点M到面α距离为 ．
5．正方形ABCD-ABCD中，E为D D中点，则B D和平面ACE位置关系是
．
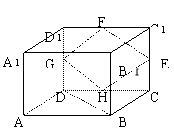6．如图，正四棱柱ABCD-AB
CD中，E、F、G、H分别是棱CC、CD、DD、DC中点，N是BC中点，
点M在四边形EFGH及其内部运动，则
M满足 时，有MN∥平面BBD D．
7．直线L上有两点到平面α距离相等，那么直线L与平面α位置关系为 ．
8．长方形ABCD-ABCD中，棱A A=5，AB=12，则直线BC与平面ABCD距离为
．
三、解答题
9．四面体ABCD被一个平面所截，截面EFGH是一个矩形
（1）求证：CD∥平面EFGH．（2）求异面直线AB和CD成角．
反思回顾
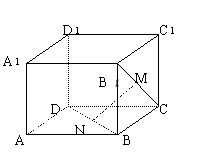10．如图，正方形ABCD-ABCD中，点N在BD上，点M在BC上，且CM=DN，求证：MN∥平面A A BB．
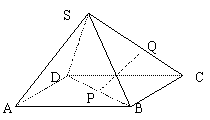
11．如图正四棱锥S-ABCD底面边长为a，侧棱长为2a，P、Q分别在BD和SC上，并且BP：PD=1：2，PQ∥平面SAD，求线段PQ长．
四、思考题
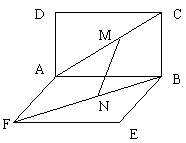
12．如图所示：正方形ABCD与正方形ABEF在平面互相垂直，两个正方形边长均为
，M、N分别是AC和BF上点，且AM=FN=x．
（1）求证：MN∥平面BCE．
（2）设MN=y，求函数y=f（x）．
（3）当MN最短时，求MN与
AC及MN与FB成角．
反思回顾
第24课时 直线和平面垂直
一、选择题
1．关于直线a、b、l与平面M、N，下列命题中正确的是 （ ）
A．若a∥M，b∥M，则a∥b B．若a∥M，b⊥a，则b⊥M
C．若aM，bM，则l⊥a，l⊥b，则l⊥M
D．若a⊥M，a∥N，则M⊥N
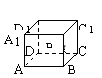2．如右图，在正方形ABCD-ABCD中，P是侧面BBCC内一点，
若P到直线BC与直线CD距离相等，则动点P的
轨迹所在曲线是 （ ）
A．直线 B．圆 C．双曲线 D．抛物线
3．三棱锥的三条侧棱两两垂直，那么这个三棱锥顶点在底面三角形所在平面上射影O必是地面三角形的 （ ）
A．内心 B．外心 C．垂心 D．重心
二、填空题
4．如图，在矩形ABCD边AB=a，BC=2，PA平面ABCD，PA=2，现有数据：①a=
②a=1③a=
④a=2 ⑤a=4，当在BC边上存在点θ,使Pθ= θD时，θ可以取
．（填上你认为正确序号）
 | |||||
 | |||||
 | |||||
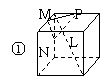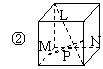5．五个正方体图形中，L是正方体一条对角线，点M、N、P分别为棱的中点，能得出L⊥面MNP图形序号是 ．
 | |||||
 | |||||
 | |||||
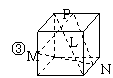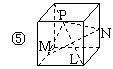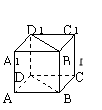6．如图，四棱柱ABCD-ABCD
的底面ABCD为正方形，侧棱与底面边长均为2a且∠AAD=∠AAB=60°，则侧棱
AA和截面BDDB距离是
．
7．α、β是两个不同的平面，m、n是平面α和β之外的两条不同直线，给出四个论断：①m⊥n ②α⊥β ③n⊥β ④m⊥α，以其中三个论断为条件，余下一个论断作为结论，写出你认为正确的一个命题 ．
8．在棱长为3的直三棱柱ABC-ABC中，M是AB上一点，AM=1，则M到BC距离为
．
反思回顾
三、解答题
9．已知PA⊥ABCD，且ABCD为矩形，M、N分别是AB、PC中点，求证：MN⊥AB．
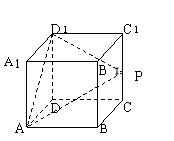10．在棱长为4的正方体ABCD-ABCD中，O是正方形ABCD中心，点P在棱CC上且CC=4CP．
（1）求直线AP与面BCCB成角；
（2）设O点在面DAP上的射影为
H，求证DH⊥AP；
（3）求P到平面ABD距离．
11．如图，ABCD是矩形，AB=a，BC=b（a＞b），沿对角线AC把△ADC折起，使AD⊥BC．
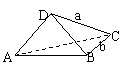（1）求证：BD是异面直线AD与BC公垂线段；
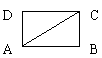（2）BD的长．
四、思考题
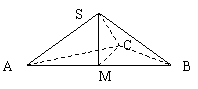12．在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=
，M为AB中点．
（1）求证AC⊥SB．
（2）求二面角S-CM-A大小．
（3）求点B到平面SCM距离．
反思回顾
第25课时 直线和平面成的角
一、选择题
1．若直线L与平面α成角为
，直线a面α，且与直线L异面，则直线L与直线a成角的取值范围是
（ ）
A．[0，
] B．[，] C．[
，]
D．[，]
2．从平面α外一点P向平面α引垂线和斜线，A为垂足，射线BC面α，且
PBC钝角，设PBC=x，ABC=y，则有
（ ）
A．x＞y B．x=y C．x＜y D．x、y大小不确定
3．若二面角α-l-β为120°，直线m⊥面α，则β所在平面内的直线与m
成角取值范围是 （ ）
A．[0°，90°] B．[30°，60°] C．[60°，90°] D．[30°，90°]
二、填空题
4．“斜线段相等”是“射影线段相等”的 条件．
5．在正三棱柱ABC-ABC中，已知AB=1，D在棱B B上，且BD=1，若AD与平面AACC成角为α，则Sinα=
.
 | |||
 | |||
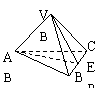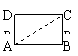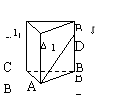
6．如上图，在底面边长为2的正三棱锥V-ABC中，E为BC中点，若△VAE面积为，则侧棱VA与底面成角为 .（结果用反三角函数表示）
7．如上图，矩形ABCD中，AB=4，BC=3，沿AC把△DAC折起，当四面体DABC的体积最大时，直线AD与平面ABC成角正弦值是 .
8．已知直线a与平面α成角为30°，点B为平面α内一定点，且Bb，ba，直线b和直线a所成角θ为定值，如这样的直线b有且只有一条，则θ的所有可能值是
.
三、解答题
9．在三棱锥P-ABC中，PA⊥AC，PB⊥BC，AC⊥BC，PA、PB与平面ABC成角为30°和45°．
（1）若P到底面ABC的距离为h，求P到AB距离．
（2）问直线PC与AB能否垂直？为什么？
反思回顾
10．如图，ACB=90°，在平面α内，PC与CA、CB成角PCA=PCB
=60°，求PC与平面α所成角．
 |
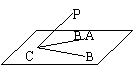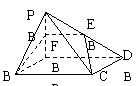11．如图，四棱锥P-ABCD的底面ABCD是边长为2的正方形，侧面PAB是正三角形，且与底面垂直，E为PD中点，过直线BC和点E的平面与侧棱PA交于点F．
（1）求证：EF∥AD．
（2）求PC和平面BCEF成角正弦值．
四、思考题
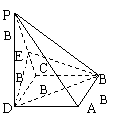12．在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E为PC中点．
（1）求证：PA∥平面EDB．
（2）求EB和底面ABCD成角正切值．
反思回顾
26课时 两个平面的平行与垂直（1）
一、选择题
1．α和β是两个不重合的平面，在下列条件中可以判定α∥β的是 （ ）
A．α、β都垂直于平面
B．α内不共线的三点到β的距离相等
C．l、m是α内的直线，且l∥β，m∥β
D．l、m是两条异面直线，且l∥α，m∥α，m∥β，l∥β
2．已知直线l⊥平面α，直线m平面β，有下列四个命题：①α∥β
l⊥m ②α⊥β l∥m
③l∥mα⊥β ④l⊥mα∥β，其中正确的两个命题是
（ ）
A．①与② B．③与④ C．②与④ D．①与③
3．α、β、是三个两两平行的平面，且α与β之间的距离是3，α与之间的距离是4，则β与之间的距离的取值范围是
（ ）
A．{1} B．{7} C．{1，7} D．[1，7]
二、填空题
4．已知空间不共面的4个点，与此四点距离相等的平面有_______ 个．
5．α∥β，A、Cα，B、Dβ，直线AB与CD交于点S，且AS=8，BS=9，CD=34，则SC=_______ ．
6．P是正方形ABCD所在平面外一点，PA⊥面ABCD，连接PB、PC、PD、AC、BD，则该几何体中互相垂直的平面共有_______ 对．
7．三个平面两两垂直，它们的交线交于一点O，且一点P到三个平面的距离分别是3、4、5，则OP=_______ ．
8．A为直二面角α-l-β棱上一点，两条长等于a的线条AB、AC分别在α、β内，且与l都成45°，则BC长为_______ ．
三、解答题
9．正方形ABCD-ABCD中M、N分别为棱AB、AD的中点，E、F分别为棱BC、CD的中点，求证平面AMN∥平面EFDB．
反思回顾
10．已知平面α∥β∥，A、Dα，C、F，AC、DF分别交于平面β于B、E．
(1)求证：
= 
．
(2)设AF交β于M，若AB：BC=1，异面直线AD与CF所成的角为60°，AD=2，CF=4，求
．
11．已知点P在平面ABC外，△ABC是等腰直角三角形，ABC=90°，△PAB是正三角形，PA⊥BC．
(1)求证：平面PAB⊥平面ABC．
(2)求二面角P-AC-B的大小．
四、思考题
12．如图ABCD是正方形，E、F分别是AD、BC边上的点，EF∥AB，EF交AC于O，以EF为棱把它折成直二面角A-EF-D后，求证不论EF怎样移动，AOC为定值．
 |
反思回顾
第27课时 两个平面的平行与垂直（2）
一、选择题
1．自大于90°的二面角内一点分别向两个面引垂线，它们所成的角与二面角的平面角的大小关系是 （ ）
A．相等 B．互补 C．相等或互补 D．无关
2．已知平面α∥平面β，它们之间的距离为d，直线aα，则在β内与直线a相距为2d的直线有
（ ）
A．一条 B．两条 C．无数条 D．不存在
3．二面角α-MN-β的平面角为
，ABα、BMN、ABM=
（为锐角），AB与面β所成角为
，则下列关系式成立的是 （ ）
A．
B．
C．
D．
二、填空题
4．菱形MNPQ的边长为a，QMN=60°，将这菱形沿对角线NQ翻折成60°的二面角，则MP与NQ间的距离
.
5．把边长为a的正△ABC沿高AD折成60°的二面角，这时A到BC边的距离是 .
6．单位圆的直径AB和PQ，AOQ=
，沿AB将两个半圆折成直二面角，那么P、Q两点间的距离为
.
7．经过平面外两点作该平面的平行平面可以作 个.
8．已知a、b是两条直线，α、β是两个平面，试用这四个元素，并借助于它们之间的关系，构造出一个判断α∥β的真命题： .
三、解答题
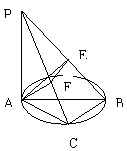
9．如图AB是⊙O的直径，C是⊙O上
的点，PA⊥平面ABC，AE⊥PB于E，
AF⊥PC于F．
求证：平面AEF⊥平面PAB.
反思回顾
10．已知PA⊥平面ABCD，ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证①MN ∥平面PAD；②平面PMC⊥平面PDC.
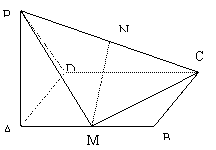
11．已知菱形ABCD的边长为2a，BAD=60°，AE、CF都垂直于平面ABCD，且AE=3a，CF=a，E、F在平面ABCD的同侧，求证平面EBD⊥平面FBD．
四、思考题
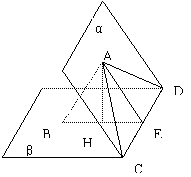
12．记二面角α-DC-β的大小为θ，设Aα，Bβ，△ADC的面积为S，且DC=m，AB⊥DC，AB与平面β成30°角，当θ取何值时，△DBC的面积有最大值，并求这个最大值．
反思回顾
第28课时 二面角（1）
一、选择题
1．下列说法正确的是 （ ）
A．二面角是两个平面相交所组成的图形
B．二面角是指角的边分别在两个平面内的角
C．角的两边分别在二面角的两个面内，则这个角是二面角的平面角
D．二面角的平面角所在平面垂直于二面角的棱
2．异面直线a、b所成的角为θ，二面角α-l-β满足a⊥α，b⊥β，则二面角α-l-β的大小为 （ ）
A．θ或π-θ B．-θ C．π-θ D．以上都有可能
3．二面角α-a-β内，过a作半平面，使二面角α-a-=45°，二面角-a-β=30°，则内的任意一点P到平面与平面的距离之比为 （ ）
A．
B． C．
D．
二、填空题
4．P是△ABC所在平面外一点，若△ABC与△PBC都是边长为2的正三角形，PA=
，那么，二面角P-BC-A的大小是
.
5．PA、PB、PC是从P点引出的三条射线，角两条的夹角都是60°，则二面角B-PA-C的余弦值是 .
6．若正三棱锥的一个侧面的面积与底面面积的比等于
，则这个三棱锥的侧面和底面所成的二面角等于
.
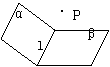7．点P是120°的二面角α-l-β内一点，
点P到α、β距离分别是3和4，则
P到l的距离为 .
8．一条直线与直二面角的两个面所成的角分别是α和β，则α+β的范围是 .
三、解答题
9．如图，已知正方形ABCD-ABCD的棱长为1.
（1）求BC
与平面ABC所成的角的正切值．
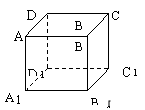（2）求二面角B- BD- C的平面角的大小．
反思回顾
10．如图，在正三棱锥ABC-ABC中，D为AC的中点.
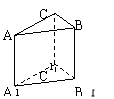（1）证明AB ∥平面D BC．
（2）假设AB⊥BC，求BC为棱，
DBC与CBC为面的二面角α
的度数．
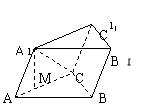11．已知斜三棱锥ABC-ABC中，BCA=90，AC=BC，A在底面ABC的射影恰为AC的中点M，又知AA与底面ABC所成的角为60°．
（1）求证：BC⊥平面AACC．
（2）求二面角B- AA - C的大小．
四、思考题
12．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥底面ABCD，且PA=AD=2a，AB=a，AC=a.
（1）求证平面PDC⊥平面PAC．
（2）求异面直线PC与BD所成的角的余弦值．
（3）设二面角A-PC-B的大小为θ，求tanθ的值.
 |
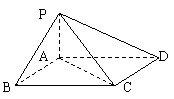反思回顾
第29课时 二面角（2）
一、选择题
1．已知二面角α-l-β的大小为60°，b和c是两条异面直线，则在下列四个条件中，能使b和c所成的叫为60°的是 （ ）
A．b∥α,c∥β B．b∥α,c⊥β
C．b⊥α,c⊥β D．b⊥α,c∥β
2．在正三角形ABC中，AD⊥BC于D,沿AD折成二面角B-AD-C后，BC=AB，这时二面角B-AD-C的大小为
（ ）
A．60° B．90° C．45° D．120°
3．矩形ABCD的两边AB=3，AD=4，PA⊥平面ABCD，且PA=
，则二面角A-BD-P的度数为
（ ）
A．30° B．45° C．60° D．75°二、填空题
4．二面角α-l-β的平面角为120°，A、Bl，ACα、BDβ，AC⊥l，BD⊥l，若AB=AC=BD=1，则CD的长为
.
5．在直角坐标系中，设A（-2，3），B（3，-2），沿X轴把直角坐标平面折成大小为θ的二面角后，
=
，则θ的值为
.
6．空间一点P到二面角α-l-β的两个面的距离分别是1和，到棱的距离是2，则二面角的大小为 .
7．二面角α-AB-β的平面角是锐角，C是平面α内的点（不在棱AB上），D是C在平面β上的射影，E是棱AB上满足CEB为锐角的任意一点，则CEB与DEB的大小关系为
.
8．正方形ABCD-ABCD中，E、F分别为B
C、CD的中点，若截面EFDB与侧面BC C B所成锐二面角为θ，则cosθ=
.
三、解答题
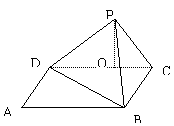9．在矩形ABCD中，AB=6，BC=
，沿对角线BD将△ABD向上折起，使点A移至点P且P在平面BCD的射影O在DC上。
（1）求证：PD⊥PC．
（2）求二面角P-BD-C的
平面角的余弦值．
反思回顾
10．如图，二面角M-l-N大小为θ，Rt△ABC在面M内，斜边AB在l上，直角边AC，BC与平面N所成角分别为α、β，求证：
+ 
= 
．
11．如图，四边形ABCD是边长为6的正方形，已知SA⊥平面ABCD，且SA=8，M是SA的中点，过M和CD的平面交SB于N，求：
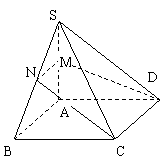（1）二面角M-DC-B的大小．
（2）求CN与平面ABCD所成角的大小．
（3）求两侧面SBC与SDC所成角的大小．
四、思考题
12．如图，梯形BCDQ中，BC∥QD，BC=1，QD=4，过点B的高BA=1，且点A平分QD，将△QBA沿AB折起，折起后点Q的位置为P，且使平面PAB⊥平面ABCD。
（1）求证：平面PCD⊥平面PAC．
（2）求直线AD和平面PCD所成角的大小．
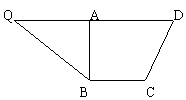（3）求二面角A-PD-C的大小．
反思回顾
第30课时 棱柱、棱锥和多面体（1）
一、选择题
1．若棱柱的侧面都是全等的矩形 ，则棱柱是 （ ）
A．直棱柱 B．正棱柱 C．正方体 D．底面是菱形的棱柱
2．三棱锥的三条侧棱两两互相垂直，则顶点在底面的射影是底面三角形的 （ ）
A．内心 B．外心 C．重心 D．垂心
3．设
，
，
，
，则这四个集合的关系是
（ ）
A．Q ⊉ M ⊉ N ⊉ P B．Q ⊈ M ⊈ N ⊈ P
C．P ⊈ M ⊈ N ⊈ Q D．Q ⊈ N ⊈ M ⊈ P
二、填空题
4．三棱锥
的三条侧棱 两两互相垂直，
为底面上一点，到三个侧面的距离分别为
则到顶点
的距离是
．
5．已知棱柱的直截面的周长为
侧棱长为
，则棱柱的侧面积为
．
6．每个顶点都有三条棱的正多面体共有 种．
7．三棱锥各侧面与底面所成的角均为
，底面三角形的三边长分别为
则此三棱锥的全面积为
．
8．一个棱锥被平行与底面的平面所截，如果截面面积与底面面积之比为1：2，那么这截面所截得的棱锥与原棱锥的体积比为 ．
三、解答题
9．已知正三棱柱
侧面的三条对角线
，若
，求证：
．
反思回顾
10．棱锥的底面是菱形，其对角线的长分别为
顶点在底面上的射影是菱形的对角线的交点，该棱锥的高是
求它的侧面积．
11．四棱锥
中，
，
是正方形，
是
的中点，过
和的截面交
于
，
，求四棱锥
的体积．
四、思考题
12．已知四棱锥
中，底面为平行四边形，侧棱
，又
，
与
所成的角为
，
求证四棱锥的体积
．
反思回顾
第31课时 棱柱、棱锥和多面体（2）
一、选择题
1．在三棱柱中，
分别是
上的点，且
，则棱锥
与原三棱柱的体积之比
（ ）
A．
B．
C．
D．
2．若三棱锥的顶点在底面内的射影恰是底面三角形的垂心，则 （ ）
A．三条侧棱的长都相等 B．三个侧面与底面所成的角都相等
C．三条侧棱必两两垂直
D．至少有两条侧棱分别与相对的底面三角形的一边互相垂直
3．一个多面体共有10个顶点，每个顶点处都有四条棱，面的形状只有三角形和四边形，则多面体有三角形和四边形的面分别为 （ ）
A．4个，8个 B．8个，4个 C．5个，6个 D．6个，5个
二、填空题
4．平行六面体各棱长都是4，在交于点三条棱上，分别有截点
且使 
则棱锥的体积是平行六面体体积的
．
5．在长方体
中，已知顶点
上三条棱 长分别是
，如果对角线
与过点的相邻三条棱所成的角分别是
那么cos
+cos
+cos
= ．
又如果对角线与过点的相邻三个面所成的角分别为
那么
．
6．已知四棱锥的底面是边长为1的正方形，
，且
，则sin∠APD=
．
7．有一个棱长为1
的 正方体容器，在过顶点
的三条棱
的中点各有一个小孔，若这个容器可以任意放量，则这个容器可装液体的最大容积为
．
8．三棱锥甲的一个侧面与三棱锥乙的一个侧面是全等的三角形。
将这两个全等三角形重合，所得新多面体的面数是 ．
三、解答题
9．在正三棱锥中，
为
的中点，且
，求异面直线
与
所成的角的余弦值．
反思回顾
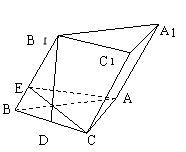10．如图，斜三棱柱的底面为直角三角形
，
，点
在下底面上的射影 
恰为
的中点，侧棱与底面成角，侧面
与侧面
成的二面角为
，求此斜三棱柱的侧面积和体积．
11．四棱锥中，侧面
是边长为2的正三角形，且与底面垂直，底面是面积为
的菱形，
为菱形的锐角．
（1）求证
．
（2）求二面角
的度数．
四、思考题
12．正三棱锥
的底面边长为2，侧棱长为3，过底面边的截面交侧棱
于，求截面
的面积的最小值．
反思回顾
第32课时 球
一、选择题
1．两个半径为1的铁球，熔化成一个球，这个大球的半径为 （ ）
A．2
B．
C．
D．
2．设地球半径为
，在北纬圈上有甲乙两地，它们的经度相差
，则这两地的纬度线之长为
（ ）
A．
B．
C．
D．
3．已知一个多面体的内切球的半径为1，多面体的表面积为18，则多面体的体积为（ ）
A．18
B．12
C．6
D．
二、填空题
4．如果球的半径扩大为原来的n倍，则球的表面积扩大为原来的 倍．
5．在球内有相距
的两个平行截面，截面面积分别是
和
，则球面积为
．
6．已知球的内接正方体的棱长为2，则此球的体积是 ．
7．一个四面体的所有棱长都为，四个顶点在同一球面上，则此球的表面积为
．
8．将一个铜球放入底面半径为
的圆柱玻璃容器中，水面升高
，则这个铜球的半径为
．
三、解答题
9．是球面上三点，已知弦AB=18cm，BC=24cm，AC=30cm．平面
与球心的距离恰好为球半径的一半，求球的表面积．
反思回顾
10．已知球
的表面上有
四点，且
两两互相垂直，若
求这个球的体积．
11．已知球的体积为
，在它里面有一个轴截面顶角为
的内接圆锥，求圆锥的体积．
四、思考题
12．求棱长为
的正八面体的内切球和外接球的体积．
反思回顾