空间向量的坐标运算

空间向量的坐标运算

一、知识回顾：

1、如果空间一个基底的三个向量互相垂直，且长都为1，则这个基底叫做　　　　　　　　　　；
常用　　　　　　　　　　 来表示。

2、在单位正交基底，，中，与向量对应的有序实数组叫做　　　　　　　　；
其中x叫做　　　　　 　　　　　 ；y叫做　　　　　　　　　 ；z叫做　　　　　　　　　 。

3、设，，则+=　　　　　　　　　　 ；=　　　　　　 　　　 ；
　　　　　　　　　 ；　　　　　　　　　　 ；∥　　　　　　　　；　　　　　　　 。

4、设，，则　　　　　，　 ，=　　　　　　。

5、在空间直角坐标系中，若，，则　　　　　　　　　　　。

6、如果表示向量的有向线段所在直线垂直于平面，则称这个向量　　　　　　　 　　　　 ；
向量叫做平面的　　　　　　　　 。

二、基础练习：

1、空间直角坐标系中，x轴上的点的坐标为　 　　　　　 ，y轴上的点的坐标为 　　　　　 ，
z轴上的点的坐标为　　　　　。

2、向量=与坐标平面　　　　 　平行；向量=与坐标平面　　　　　平行。

3、若向量=，=，且与垂直，则　　　。

4、已知点B是点在平面上的射影，则 　　　　　　　　　　 。

5、若向量与向量共线，且满足，则=　　　　　　　。

6、同时垂直于=，=的单位向量为　　　　　　　　 。

三、典型例题：

1、已知△ABC的三顶点，，，求（1）△ABC的重心坐标；
（2）BC边上的中线长；（3）∠A的余弦值；（4）△ABC的面积。

2、已知四边形ABCD的顶点分别是，，，
求证：四边形ABCD是一个梯形。

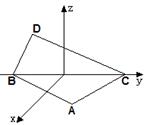
3、如图，在空间直角坐标系中，BC=2，O是BC的中点，点A的坐标是，点D在平面yOz上，且∠BDC=90º，∠DCB=30º，
求（1）向量的坐标；（2）设向量和的夹角为，求。

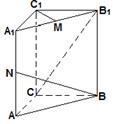
4、直三棱柱ABC-A₁B₁C₁中，CA=CB=1，∠BCA=90º，AA₁=2，
M、N分别是A₁B₁、AA₁的中点，
（1）求NB的长；（2）求；（3）求证：

四、巩固练习：

1、设点B是点A关于面的对称点，则 　　　　　　　　　　 。

2、已知，，，若A、B、C三点共线，则　 。

3、在坐标平面yOz内，与三个已知点A（3,1,2），B（4,-2,-2），C（0,5,1）等距离的点D的坐标是　　　　　　　　　 。

4、设向量=，=，（1）求，及与所成的角；
（2）确定，的关系，使与z轴垂直。

5、A(0,2,3)，B(-2,1,6)，C(1,-1,5)为空间三点，（1）求以，为边的平行四边形面积；（2）若，且分别与，垂直，求向量的坐标。

6、正方体ABCD-A₁B₁C₁D₁中，E、F分别是BB₁、DC的中点，
（1）求直线AE和D₁F所成的角；（2）证明：AE⊥平面A₁D₁F