上学期期中考试高二数学试题2
一、选择题: (每小题5分，共计50分，请将正确答案写在答案纸上)
1、(1)底面是正多边形的棱锥一定是正棱锥；
(2)正棱柱的侧面是正方形；
(3)底面是平行四边形的四棱柱叫平行六面体；
(4)正多面体的各个面都是正三角形. 其中正确的命题有 （ ）
A、0个 B、1个 C、2个 D、3个
2、用平行于底面的平面去截棱锥，将该棱锥分成体积相等的两部分，则截面把棱锥的高分成自上而下的两段长度之比为 （ ）
A、1∶
B、∶
D、∶1
3、五名运动员去争夺
、跳高、跳远三项冠军，则冠军的可能情形共有 （ ）
A、
种 B、
种 C、
种 D、
种
4、举办一台文艺晚会，先要排一个节目单，现有9个歌唱节目，5个舞蹈节目，4个相声节目，要求4个相声节目不连排，也不排在第一个，共可排出节目单的个数为 ( )
A、
B、
C、
D、
5、若长方体一条对角线与交于一点的三条棱所成角分别为45°、60°、
，则角= ( )
A、30° B、45° C、60° D、75°
6、斜三棱柱ABC-
各条棱长均为a，侧棱
与底棱AB、AC均成60°角，则侧面
的面积为
（ ）
A、
B、
C、
D、
7、棱长为a的正四面体，设其内切球半径r，则r与a的关系为 ( )
A、
B、
C、
D、
8、
，
，方程
表示焦点在
轴上椭圆，则共有 ( )
A、15个 B、14个 C、13个 D、12个
9、设
，则
等于
( )
A、
B、
D、
10、某种化学实验中需依次投放化工原料，现有6种原料可供选用，但甲、乙两种原料不能同时使用，且每次都是依次投放2种原料，若使用甲原料时，则甲必须先投入，因此不同的实验方案有 （ ）
A、19种 B、24种 C、34种 D、14种
二、填空题:(每小题5分，共计30分，请将正确答案写在答案纸上)
11、从4名男生和3名女生中选出4人参加辩论比赛，如果男生中的甲与女生中的乙必须在内，有 种选法.
12、由0,1,2,3,4,5这六个数字共可组成 个无重复数字的三位偶数.
13、一个简单多面体各个顶点都有三条棱，则
.
14、已知球面上有三点A，B，C且AB=6cm，BC=8cm，CA=10cm，则球心到平面ABC距离为7cm，则此球的表面积为 .
15、考虑一元二次方程
，其中系数
，
的取值是随机的，分别等于将一枚骰子连掷两次先后出现的点数，则方程有实根的概率为
.
16、在底边长为
,高为的正四棱柱中，以它各面的中心为顶点可得一个八面体，则该八面体的体积为
.
三、解答题：(本大题共6小题，满分70，解答应写出文字说明，证明过程或演算步骤)
17、在以AB为直径的半圆周上，有异于A、B的六个点
、
……
,在直径AB上有异于A、B的四个点
、
、
、
.
试问: (1)以这10个点中的3个点为顶点作三角形，一共可作多少个？
(2)在(1)中含有点的三角形有多少个 ? (10分)
18、一个袋中有4个白球，5个黑球，连续从中取出3个球,求:
(1)取后放回且顺序为黑白黑的概率
(2)取后不放回且取出2黑1白的概率(12分)
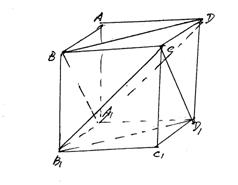19、如图,正方体
的棱长为,
求证：(1)平面
∥
;(2)
⊥平面
;
(3)对角线
被平面
和平面
三等分.(12分）
20、在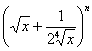
展开式中，已知前三项的系数成等差数列，求n及展开式中所有的有理项(12分)
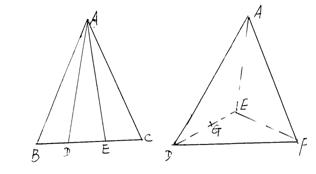
21、已知正
的边长为3，D、E分别是BC上的三等分点，沿AD、AE把折成三棱锥A-DEF，使B、C两点重合于点F，且G是DE的中点.
(1)求二面角A-DE-F的大小
(2)求点F到平面ADE的距离(12分)
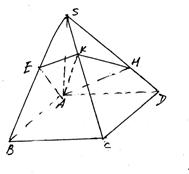
22、已知：如图,四边形ABCD是正方形，
⊥平面ABCD，且
，过点A作与
垂直的平面分别交
、
、
于点E、K、H.
(1)求与平面
所成角的正切值；
(2)求证：
⊥
.（12分）