高二数学期末复习（椭圆一）
1．椭圆的对称轴为坐标轴，若长、短轴之和为18，焦距为6，那么椭圆的方程为（ ）
（A）
（B）
（C）或
（D）
2．曲线
与
(k<9)有相同的（ ）
（A）短轴 （B）焦点 （C）离心率（D）不能确定
3．椭圆
(a>b>0)的左焦点F到过顶点A(－a, 0), B(0, b)的直线的距离等于
，则椭圆的离心率为（ ）
（A）
（B）
（C）
（D）
4．离心率为
，长轴长为6的椭圆的标准方程是（ ）
（A）
（B）或
（C）
（D）或
5．椭圆
上有n个不同的点P1, P2, P3,……, Pn，椭圆的右焦点为F，数列{PnF}是公差大于
的等差数列，则n的最大值为
（ ）
（A）199 （B）200 （C）198 （D）201
6．点P是长轴在x轴上的椭圆上的点，F1, F2分别为椭圆的两个焦点，椭圆的半焦距为c，则PF1·PF2的最大值与最小值之差一定是（ ）
（A）1 （B）a2 （C）b2 （D）c2
7．一个圆心在椭圆右焦点F2，且过椭圆的中心O(0, 0)，该圆与椭圆交于点P，设F1是椭圆的左焦点，直线PF1恰和圆相切于点P，则椭圆的离心率是（ ）
（A）
－1
（B）2－ （C）
（D）
8．设F1(－c, 0), F2(c, 0)是椭圆(a>b>0)的两个焦点，P是以F
（A）
（B） （C） （D）
9．椭圆
和
具有 （ ）
A．相同的离心率 B．相同的焦点 C．相同的顶点 D．相同的长、短轴
10．椭圆
上的点到直线
的最大距离是（
）
A．3 B．
C．
D．
11．过点M（－2，0）的直线m与椭圆
交于P1，P2，线段P1P2的中点为P，设直线m的斜率为k1（
），直线OP的斜率为k2，则k1k2的值为 （ ）
A．2 B．－ D．－
12．椭圆上的点到直线的最大距离是（
）
A．3 B． C． D．
13．已知△ABC的周长是8，B、C的坐标分别是（
，0）和（1，0），则顶点A的轨迹方程是（ ）
A、
）B、
C、
D、
14．若椭圆
的离心率为e=，则k的值等于
.
15．若椭圆的一短轴端点与两焦点连线成120°角，则该椭圆的离心率为 .
16．椭圆
上一点P与椭圆两焦点F1, F2的连线的夹角为直角，则Rt△PF
17．已知椭圆Ｅ的短轴长为6，焦点Ｆ到长轴的一个端点的距离等于９，则椭圆Ｅ的离心率等于
18．（06年上海卷）已知椭圆中心在原点，一个焦点为F（－2，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 ．
19.（05上海）若椭圆长轴长与短轴长之比为2，它的一个焦点是(2
,0),则椭圆的标准方程是
高二数学期末复习（椭圆二）
1．椭圆的对称轴为坐标轴，若长、短轴之和为18，焦距为6，那么椭圆的方程为（ ）
（A） （B） （C）或 （D）
2．曲线与 (k<9)有相同的（ ）
（A）短轴 （B）焦点 （C）离心率（D）不能确定
3．椭圆(a>b>0)的左焦点F到过顶点A(－a, 0), B(0, b)的直线的距离等于，则椭圆的离心率为（ ）
（A） （B） （C） （D）
4．离心率为，长轴长为6的椭圆的标准方程是（ ）
（A） （B）或
（C） （D）或
5．椭圆上有n个不同的点P1, P2, P3,……, Pn，椭圆的右焦点为F，数列{PnF}是公差大于的等差数列，则n的最大值为
（ ）
（A）199 （B）200 （C）198 （D）201
6．点P是长轴在x轴上的椭圆上的点，F1, F2分别为椭圆的两个焦点，椭圆的半焦距为c，则PF1·PF2的最大值与最小值之差一定是（ ）
（A）1 （B）a2 （C）b2 （D）c2
7．一个圆心在椭圆右焦点F2，且过椭圆的中心O(0, 0)，该圆与椭圆交于点P，设F1是椭圆的左焦点，直线PF1恰和圆相切于点P，则椭圆的离心率是（ ）
（A）－1
（B）2－ （C） （D）
8．设F1(－c, 0), F2(c, 0)是椭圆(a>b>0)的两个焦点，P是以F
（A） （B） （C） （D）
9．椭圆和具有 （ ）
A．相同的离心率 B．相同的焦点 C．相同的顶点 D．相同的长、短轴
10．椭圆上的点到直线的最大距离是（
）
A．3 B． C． D．
11．过点M（－2，0）的直线m与椭圆交于P1，P2，线段P1P2的中点为P，设直线m的斜率为k1（），直线OP的斜率为k2，则k1k2的值为 （ ）
A．2 B．－ D．－
12．椭圆上的点到直线的最大距离是（
）
A．3 B． C． D．
13．已知△ABC的周长是8，B、C的坐标分别是（，0）和（1，0），则顶点A的轨迹方程是（ ）
A、）B、 C、 D、
14．若椭圆的离心率为e=，则k的值等于
.
15．若椭圆的一短轴端点与两焦点连线成120°角，则该椭圆的离心率为 .
16．椭圆上一点P与椭圆两焦点F1, F2的连线的夹角为直角，则Rt△PF
17．已知椭圆Ｅ的短轴长为6，焦点Ｆ到长轴的一个端点的距离等于９，则椭圆Ｅ的离心率等于
18．（06年上海卷）已知椭圆中心在原点，一个焦点为F（－2，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 ．
19.（05上海）若椭圆长轴长与短轴长之比为2，它的一个焦点是(2,0),则椭圆的标准方程是
高二数学期末复习（双曲线1）
1． 双曲线
的焦距是 （ ）
A．4 B． C．8 D．与
有关
2.已知双曲线8kx2-ky2=8的一个焦点为（0，3），则k的值为 （ ）
（A）1 （B）-1 （C）
（D）
3.与两圆x2+y2=1和x2+y2-8x+7=0都相切的圆的圆心轨迹是( )
A.两个椭圆 B.两条双曲线 C.一条双曲线和一条直线 D.一个椭圆与一条双曲线
4.以椭圆
+
=1的焦点为顶点，以这个椭圆的长轴的端点为焦点的双曲线的方程是( )
A.-y2=1 B.y2- =-=1 D. 
-
=1
5.设动点P到定点F1(-5，0)的距离与它到定点F2(5，0)的距离的差等于6，则P点轨迹方程是( )
A. 
-
=1 B. 
-
=-=1(x≥3) D.-=1(x≤-3)
6.直线l过双曲线
-
=1的下方焦点F1且与双曲线的下支交于A、B两点，F2是双曲线的另一个焦点，且｜AB｜=m,则△ABF2的周长为( )
A
7.若动圆P与两定圆(x+5)2+y2=1及(x-5)2+y2=49都相内切或都相外切，则动圆圆心轨迹方程是( )
A. -=1 B.-=1(x＞0) C.-=1 D.-=1(x＞0)
8．过双曲线
左焦点F1的弦AB长为6，则
（F2为右焦点）的周长是（ ）
A．28
B．
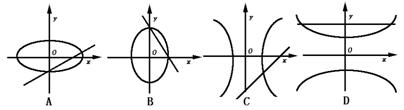
9.已知m,n为两个不相等的非零实数，则方程mx-y+n=0与nx2+my2=mn所表示的示意曲线是( )
10．P为双曲线
上一点，F1、F2为焦点，若∠F1PF2＝60°，那么△F1PF2的面积是
。
11．一条渐近线方程为3x－2y＝0，实轴长为8的双曲线方程是
16.若椭圆mx2+ny2=1(0＜m＜n)和双曲线ax2-by2=1(a＞0,b＞0)有相同的焦点F1、F2，P是两曲线的一个交点，则｜PF1｜·｜PF2｜= .
12.过点A(-2，4
)、B(3，-2
)的双曲线的标准方程为 .
13.与双曲线16x2-9y2=-144有共同焦点，且过点(0，2)的双曲线方程为 .
14.已知B(-5，0)，C(5，0)是△ABC的两个顶点，且sinB-sinC=
sinA,则顶点A的轨迹方程是 .
15.已知双曲线
-
=1(a＞0,b＞0)的弦AB的中点为M，O为坐标原点，则直线OM和直线AB的斜率的乘积为 .
16.已知双曲线x2-=1,过点P(2，1)作直线交双曲线于A、B两点，并使P为AB的中点，则｜AB｜=
.
17.若圆C过双曲线-=1的两焦点，且截直线y=-1所得弦长为8，则圆C的方程为
.
18.过点M(3，-1)且被点M平分的双曲线-y2=1的弦所在直线方程为
19.双曲线3x2-y2=1上是否存在关于直线y=2x对称的两点A、B?若存在，试求出A、B两点的坐标；若不存在，说明理由.
高二数学同步测试（双曲线2）
1．方程
表示双曲线，则
的取值范围是 （ ）
A．
B．
C．
D．
或
2．若
，双曲线
与双曲线
有 （ ）
A．相同的虚轴 B．相同的实轴 C．相同的渐近线 D． 相同的焦点
3．过双曲线左焦点F1的弦AB长为6，则（F2为右焦点）的周长是（ ）
A．28
B．
4．已知双曲线方程为
，过P（1，0）的直线L与双曲线只有一个公共点，
则L的条数共有 （ ）
A．4条 B．3条 C．2条 D．1条
5.F1、F2为双曲线
的两个焦点，点P在双曲线上，且∠F1PF2=90°,则
△F1PF2的面积是（ ）
A.2 B.4 C.8 D.16
6．下列各对曲线中，即有相同的离心率又有相同渐近线的是（ ）。
(A)
－y2=1和
－=1 (B)－y2=1和y2－=1
(C)y2－=1和x2－
=1 (D)－y2=1和－=1
7．与双曲线x2－
＝1有共同渐近线且经过点(2, 2)的双曲线方程是（ ）。
（A）
（B）
（C）－x2＝1
（D）
－x2＝1
8．以y＝±
x为渐近线，一个焦点在F(0,
2)的双曲线方程是（ ）。
（A）x2－＝1 （B）－x2＝1
（C）
（D）
9．若点 
是以 
、 
为焦点的双曲线 
上的一点，若
，则 
（ ）
A．2 B．22 C．2或22 D．4或22
10．如果 
表示焦点在 
轴上的双曲线，那么它的半焦距 
的取值范围是（ ）
A． 
B．（0，2） C． 
D．（1，2）
11.已知双曲线的离心率等于2，且过点M（2，-3），此双曲线标准方程是______.
12.中心在原点，一条渐近线方程为4x-3y=0的双曲线离心率是______
13．如果椭圆 
与双曲线 
的焦点相同，那么 
．
14．双曲线与椭圆
有公共焦点，它的一条渐近线的方程是x＋y＝0，则双曲线的方程是
15．求一条渐近线方程是
，一个焦点是
的双曲线标准方程，并求此双曲线的离心率．
16. 一炮弹在某处爆炸，在 
处听到爆炸声的时间比在 
处晚 
，（1）爆炸点应在什么样的曲线上？（2）已知 、 两地相距 
，并且此时声速为 
，求曲线的方程．
17. 已知双曲线 
的右焦点分别为 、 ，点 在双曲线上的左支上且 
，求 
的大小．
18．已知一椭圆的中心在原点，焦点在坐标轴上，焦距为
，一双曲线与此椭圆有公共焦点，且半实轴的长比椭圆的半长轴长小4，两曲线离心率之比为3∶7，求椭圆和双曲线的方程。
19．如图，OA是双曲线的实半轴，OB是虚半轴，F为焦点，且∠BAO=300，S△ABF=
， 求此双曲线方程。
高二数学期末复习（抛物线 一)
1．顶点在原点，坐标轴为对称轴的抛物线，过点
，则它的方程是（ ）
A、
B、
C、
D、
2．抛物线
的焦点坐标是（ ）
A、
B、
C、
D、
3．过抛物线
的焦点作直线交抛物线于P
，Q
两点，若
则PQ为（ ）
A、10
B、
4.直线y=kx-2交抛物线y2=8x于A、B两点，若AB中点的横坐标为2，则k等于( )
A.0 B
5.抛物线y2=2px上横坐标为6的点到焦点的距离是10，则焦点到准线距离是( )
A.4 B
6.已知P(x0,y0)是抛物线y2=2mx上的任意一点，则点P到焦点的距离是( )
A.｜x0-
｜
B.｜x0+｜
C.｜x0-m｜ D.｜x0+m｜
7．动点 到点 
的距离比到直线 
的距离小2，则动点 的轨迹方程为（ ）
A． 
B．
C．
D． 
8.F是抛物线y2=2x的焦点，P是抛物线上任一点，A(3，1)是定点，则｜PF｜+｜PA｜的最小值是( )
A.2 B.
C.3 D.
9.长度为4的线段AB的两个端点A、B都在抛物线x2=4y上，则线段AB的中点M的纵坐标的最小值为( )
A. B
10.抛物线y=x2上到直线2x-y-4=0最近的点的坐标是( )
A.(，
) B.(1，1) C.(
，
) D.(2，4)
11．抛物线焦点在
轴上,
在抛物线上且AF=5，则抛物线的标准方程为
12某桥的桥洞呈抛物线形，如图，桥下水面宽
米，水面距桥洞1.5米。降雨后测得水面宽8米，则水面上涨了
米。
13.P(x1,y1),P2(x2,y2)是过抛物线y2=2px(p＞0)的焦点的弦的两端，则y1y2= .
14．已知圆
，与抛物线
的准线相切，则
___________．
15．对于顶点在原点的抛物线，给出下列条件；
（1）焦点在y轴上； （2）焦点在x轴上；
（3）抛物线上横坐标为1的点到焦点的距离等于6；（4）抛物线的通径的长为5；
（5）由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）．
其中适合抛物线y2=10x的条件是(要求填写合适条件的序号) _
16.已知椭圆
+y2=1的焦点为F1、F2，抛物线y2=px(p＞0)与椭圆在第一象限的交点为Q，若∠F1QF2=60°，(1)求△F1QF2的面积；(2)求此抛物线的方程.
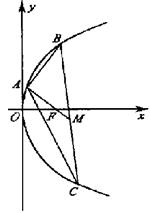17．已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线
上，△ABC的重心与此抛物线的焦点F重合（如图）
（1）写出该抛物线的方程和焦点F的坐标；
（2）求线段BC中点M的坐标；
（3）求BC所在直线的方程.
高二数学期末复习（抛物线二)
1．抛物线上有
三点，
是它的焦点，若
成等差数列，则 （
）
A．
成等差数列
B．
成等差数列
C．
成等差数列
D．
成等差数列
2．已知抛物线
的焦点弦
的两端点为
,
,则关系式
的值一定等于
（ ）
A．4p B．－4p C．p2 D．－p
3．过抛物线
的焦点F作一直线交抛物线于P，Q两点，若线段PF与FQ的长分别是
，则
（
）
A．
B．
C．
D．
4．若AB为抛物线y2=2px (p>0)的动弦，且AB=a (a>2p)，则AB的中点M到y轴的最近距离是 （ ）
A．
a B．p C．
a＋
p D．a－
p
5.过抛物线的焦点F的直线与抛物线交于A、B两点，若A、B两点在抛物线的准线上的射影是A1、B1，则∠A1FB1等于( )
A.45° B.60° C.90° D.°120
6．直线 
与抛物线 交于 
两点，且 
的中点横坐标为2，则 
的值是（ ）
A． 
B．2 C． 或2
D．以上都不对
7．平面上动点P到定点F(1, 0)的距离比到y轴的距离大1，则动点P的轨迹方程是
（A）y2=2x （B）y2=4x （C）y2=2x和y=0(x≤0) （D）y2=4x和y=0(x≤0)
8．圆心在抛物线y2=2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是
（A）x2+y2－x－2y－=0 （B）x2+y2+x－2y+1=0
（C）x2+y2－x－2y+1=0 （D）x2+y2－x－2y+=0
9．探照灯的反光镜的纵断面是抛物线的一部分，光源在抛物线的焦点处，已知灯口直径是60cm，灯深40cm，则光源到反光镜顶点的距离是
（A）11.25cm （B）5.625cm （C）20cm （D）10cm
10．动圆与定圆A: (x+2)2+y2=1外切，且和直线x=1相切，则动圆圆心的轨迹是
（A）直线 （B）椭圆 （C）双曲线 （D）抛物线
11已知F是抛物线
焦点，P是该抛物线上的动点，则线段PF中点的轨迹方程是（ ）
A．
B．
C．
D．
12．抛物线与直线
交于A、B两点，其中点A的坐标为（1，2），设抛物线的焦点为F，则FA+FB等于（ ）A．7 B．
C．6 D．5
13．有一个正三角形，它的两个顶点在抛物线y2=－4x上，另一个顶点在原点，则此正三角形的面积是 _________ .
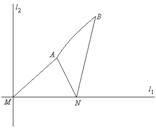
14．直线l1和l2相交于点M,
l1⊥l2，点N∈l1，以A, B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等，若△AMN为锐角三角形，且AM=
，AN=3,
BN=6, 建立适当的坐标系，求曲线C的方程。
