双曲线及其标准方程练习
一、选择题(每小题四个选项中,只有一项符合题目要求)
1.已知点![]() 和
和![]() ,曲线上的动点P到
,曲线上的动点P到![]() 、
、![]() 的距离之差为6,则曲线方程为( )
的距离之差为6,则曲线方程为( )
A.![]()
B.![]()
C.![]() 或
或![]()
D.![]()
2.“ab<0”是“方程![]() 表示双曲线”的( )
表示双曲线”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分又不必要条件
3.动圆与两圆![]() 和
和![]() 都相切,则动圆圆心的轨迹为( )
都相切,则动圆圆心的轨迹为( )
A.抛物线
B.圆
C.双曲线的一支
D.椭圆
4.P为双曲线![]() 上的一点,F为一个焦点,以PF为直径的圆与圆
上的一点,F为一个焦点,以PF为直径的圆与圆![]() 的位置关系是( )
的位置关系是( )
A.内切
B.内切或外切
C.外切
D.相离或相交
5.双曲线![]() 的左焦点为F,点P为左支的下半支上任一点(非顶点),则直线PF的斜率的范围是( )
的左焦点为F,点P为左支的下半支上任一点(非顶点),则直线PF的斜率的范围是( )
A.(-∞,0]∪[1,+∞)
B.(-∞,0)∪(1,+∞)
C.(-∞,-1)∪[1,+∞)
D.(-∞,-1)∪(1,+∞)
6.若椭圆![]() 和双曲线
和双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,P是两曲线的一个公共点,则
,P是两曲线的一个公共点,则![]() 的值是( )
的值是( )
A.m-a
B.![]()
C.![]()
D.![]()
二、填空题
7.双曲线![]() 的一个焦点是
的一个焦点是![]() ,则m的值是_________。
,则m的值是_________。
8.过双曲线![]() 的焦点且垂直于x轴的弦的长度为_______。
的焦点且垂直于x轴的弦的长度为_______。
三、解答题
9.已知双曲线过点A(-2,4)、B(4,4),它的一个焦点是![]() ,求它的另一个焦点
,求它的另一个焦点![]() 的轨迹方程。
的轨迹方程。
10.已知直线y=ax+1与双曲线![]() 相交于A、B两点,是否存在这样的实数a,使得A、B关于直线y=2x对称?如果存在,求出a的值,如果不存在,说明理由。
相交于A、B两点,是否存在这样的实数a,使得A、B关于直线y=2x对称?如果存在,求出a的值,如果不存在,说明理由。
11.A、B、C是我方三个炮兵阵地,A在B的正东相距6km,C在B的北偏西30°相距4km,P为敌炮兵阵地,某时刻A发现敌炮阵地的某种信号,4秒种后,B、C才同时发现这一信号,该信号的传播速度为每秒1km,A若炮击P地,求炮击的方位角。
答案与提示
一、1.D
2.A
3.C
4.B
5.B
6.A
二、7.-2
8.![]()
三、9.提示:易知![]()
由双曲线定义知![]()
即![]()
①![]() 即
即![]()
此时点![]() 的轨迹为线段AB的中垂线,其方程为x=1(y≠0)
的轨迹为线段AB的中垂线,其方程为x=1(y≠0)
②![]() 即
即![]()
此时点![]() 的轨迹为以A、B为焦点,长轴长为10的椭圆,其方程为
的轨迹为以A、B为焦点,长轴长为10的椭圆,其方程为![]() (y≠0)
(y≠0)
10.不存在
11.提示:以AB的中点为原点,正东、正北方向分别为x轴、y轴建立直角坐标系,则A(3,0),B(-3,0),![]() ,依题意PB-PA=4
,依题意PB-PA=4
∴ P点在以A、B为焦点的双曲线的右支上,其中c=3,2a=4,则![]() ,方程为
,方程为![]()
又PB=PC ∴P在线段BC的垂直平分线![]() 上
上
联立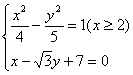 解得
解得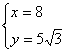 ∴
∴![]()
又![]() ∴α=60°
∴α=60°
∴P点在A点东偏北60°处,即A炮击P地时,炮击的方位角为北偏东30°