算术平均数与几何平均数练习
【同步达纲练习】
知识强化：
一、选择题
1.下列不等式中，对任意实数x都成立的是( )
A.lg(x2+1)≥lgx B.x2+1>2x
C.
≤1 D.x+
≥2
2.已知a,b∈R，且ab≠0，则在①
≥ab ②
≥2 ③ab≤(
)2 ④()2≤这四个不等式中，恒成立的个数是( )
A.1 B.2
C.3 D.4
3.已知a,b∈R+，且a+b＝1，则下列各式中恒成立的是( )
A.
≥
B.
≥4
C.
≥ D.
≤
4.函数y＝3x2+
的最小值是( )
A.3
-3` B.-3
C.6 D.6-3
5.已知x>1，y>1，且lgx+lgy＝4，则lgxlgy的最大值是( )
A.4 B.2
C.1 D.
二、填空题
6.已知a>b>c，则
与
的大小关系是 .
7.若正数a,b满足ab＝a+b+3，则ab的取值范围是 .
8.已知a,b,c∈R且a2+b2+c2＝1，则ab+bc+ca的最大值是 ，最小值是 .
三、解答题
9.已知a,b,c∈R，求证：a4+b4+c4≥a2b2+b2c2+c2a2≥abc(a+b+c).
10.(1)求y＝2x2+
(x>0)的最小值.
(2)已知a,b为常数，求y＝(x-a)2+(x-b)2的最小值.
素质优化：
一、选择题
1.已知f(x)＝()x，a,b∈R+，A＝f()，G＝f(),H＝f(
)，则A、G、H的大小关系是( )
A.A≤G≤H B.A≤H≤G
C.G≤H≤A D.H≤G≤A
2.已知x∈R+，下面各函数中，最小值为2的是( )
A.y＝x+ B.y＝
+
C.y＝x+
D.y＝x2-2x+4
3.当点(x,y)在直线x+3y-2＝0上移动时，表达式3x+27y+1的最小值是( )
A.3
B.1+2
C.6 D.7
4.设M＝(
-1)(
-1)(
-1)
，且a+b+c＝1，(其中a,b,c∈R+)，则M的取值范围是( )
A.［0，
］ B.［，1］
C.［1，8］ D.［8，+∞)
5.若a,b,c,d,x,y∈R+，且x2＝a2+b2,y2＝c2+d2，则下列不等式中正确的是( )
A.xy<ac+bd B.xy≥ac+bd
C.xy>ac+bd D.xy≤ac+bd
二、填空题
6.斜边为8的直角三角形面积的最大值是 .
7.已知x,y,∈R+，且xy2＝4，则x+2y的最小值是 .
8.设x>y>z,n∈N，且
≥
恒成立，则n的最大值是 .
三、解答题
9.设n∈N，求证
+…+
<
.
10.证明，任何面积等于1的凸四边形的周长及两条对角线的长度之和不小于4+2.
创新深化：
一、选择题
1.设x∈R，且满足
+
＝cosθ，则实数θ的值为( )
A.2kn(k∈Z) B.(2k+1)π(k∈Z)
C.kn(k∈Z) D.kn+
(k∈Z)
2.对一切正数m，不等式n<
+2m2恒成立，则常数n的取值范围是( )
A.(-∞，0) B.(-∞，6)
C.(6，+∞) D.［6，+∞)
3.若a,b,c∈R，且ab+bc+ca＝1，则下列不等式成立的是( )
A.a2+b2+c2≥2 B.(a+b+c)2≥3
C.
≥2
D.abc(a+b+c)≤3
4.已知a,b是不相等的正数，在a,b之间插入两组数x1,x2,…,xn，和y1,y2,…，yn，使a,x1,x2,…,xn,b成等差数列，a,y1,y2,…,yn,b成等比数列，并给出下列不等式.
①
(x1+x2+…+xn)>(
)2
② (x1+x2+…+xn)>
③
<
④<(
)2
则其中为真命题的是( )
A.①③ B.①④
C.②③ D.②④
5.某种汽车购车时费用为10万元，每年的保险、养路、汽油费用共9千元，汽车的维修费逐年以等差数列递增，第一年为2千元，第2年为4千元，第三年为6千元，……问这种汽车使用几年后报废最合算?(即汽车的平均费用为最低)( )
A.8年 B.9年
C.10年 D.11年
二、填空题
6.已知0<x<1，a、b为正常数，则y＝
的最小值是 .
7.已知a,b∈R，且a>
>0，则a+
的最小值是 .
8.sin4αcos2α的最大值是 ，此时，sinα＝ ,cosα＝ .
三、解答题
9.在两个正数x、y之间，插入一个正数a，设x，a，y成等比数列，另插入两个正数b,c,设x,b,c,y成等差数列，求证：(a+1)2≤(b+1)(c+1).
10.已知a>0,b>0,c>0,a+b+c＝1.求证：(1+)(1+)(1+)≥64.
参考答案
【同步达纲练习】
知识强化：
1.C 2.C 3.B 4.D 5.A
6.
≤ 7.［9,+∞) 8.1，- 9.∵a4+b4≥2a2b2,b4+c4≥2b2c2,c4+a4≥2c2a2相加得a4+b4+c4≥a2b2+b2c2+c2a2,∵a2b2+b2c2≥2b2ac,b2c2+c2a2≥2c2ab,c2a2+a2b2≥2a2bc相加得a2b2+b2c2+c2a2≥b2ac+c2ab+a2bc＝abc(a+b+c). 10.(1)y＝2x2+
+≥3
.(2)y＝(x-a)2+(b-x)2≥
素质优化:
1.A 2.A 3.D 4.D 5.B
6.16 7.3
8.4 9.左边<
+…+
(1+2+…+n)+［2+3,+…+(n+1)］＝
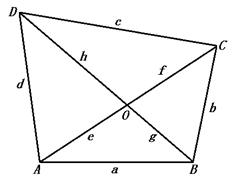
10.如图，设凸四边形ABCD边长依次为a,b,c,d，对角线AC与BD交于O点，设AO＝e，CO＝f，BO＝g，DO＝h.∴1＝SABCD＝(eg+gf+fh+he)sin∠AOB≤(e+f)(g+h)≤(
)2,∴e+f+g+h≥
＝2.又2＝2SABCD＝absinB+bcsinc+cdsinD+dasinA≤(ab+bc+cd+da)＝(a+c)(b+d)≤ (
)2,∴a+b+c+d≥4，从而命题得证.
创新深化:
1.C 2.B 3.B 4.B 5.C
6.(a+b)2
7.
8.
，±
,±
9.依题意
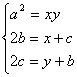,即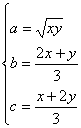
,∴(b+1)(c+1)＝bc+b+c+1＝
+x+y+1＝
［2(x2+y2)+5xy］+(x+y)+1≥ (4xy+5xy)+2
+1＝(+1)2＝(a+1)2.
10.∵a>0,b>0,c>0,a+b+c＝1,∴1＝a+b+c≥
,∴abc≤
,即
≥27，∴(1+)(1+)(1+)＝1+(++)+(+
+
)+≥1+3
+3
+≥1+9+27+27＝64.