椭圆的简单几何性质练习
一、选择题(每小题四个选项中,只有一项符合题目要求)
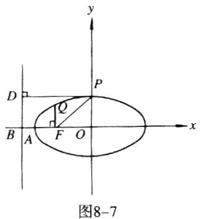
1.如图8-7,点O是椭圆中心,F为焦点,A为顶点,准线l交x轴于B,P、Q在椭圆上且PD⊥l于D,QF⊥AO于F。关于曲线的离心率有如下数值:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() 。其中正确的个数是( )
。其中正确的个数是( )
A.2
B.3
C.4
D.5
2.一个圆的圆心在椭圆的右焦点![]() 上,且过椭圆的中心D(0,0),该圆与椭圆交于点P,设
上,且过椭圆的中心D(0,0),该圆与椭圆交于点P,设![]() 是椭圆的左焦点,直线
是椭圆的左焦点,直线![]() 恰好与圆相切于点P,则椭圆的离心率是( )
恰好与圆相切于点P,则椭圆的离心率是( )
A.![]()
B.![]()
C.![]()
D.![]()
3.过原点的椭圆的一个焦点为F(1,0),其长轴长为4,则另一个焦点的轨迹方程为( )
A.![]()
B.![]()
C.![]()
D.![]()
4.点M与椭圆![]() 的左焦点和右焦点的距离之比为2∶3,则点M的轨迹方程为( )
的左焦点和右焦点的距离之比为2∶3,则点M的轨迹方程为( )
A.![]()
B.![]()
C.![]()
D.![]()
5.设点![]() ,F为椭圆
,F为椭圆![]() 的右焦点,点M在该椭圆上移动,当AM+2MF取最小值时,点M的坐标是( )
的右焦点,点M在该椭圆上移动,当AM+2MF取最小值时,点M的坐标是( )
A.![]()
B.![]()
C.![]()
D.![]()
二、填空题
6.一个椭圆的离心率为![]() ,一个焦点为F(3,0),对应的准线为x-1=0,则这个椭圆的方程为__________。
,一个焦点为F(3,0),对应的准线为x-1=0,则这个椭圆的方程为__________。
7.过椭圆![]() 的左焦点作一条长为
的左焦点作一条长为![]() 的弦AB,将椭圆绕着其左准线在空间旋转120°,则弦AB扫过的面积为_________。
的弦AB,将椭圆绕着其左准线在空间旋转120°,则弦AB扫过的面积为_________。
三、解答题
8.过椭圆![]() 的一个焦点的直线交椭圆于A、B两点,求△AOB的面积的最大值(O为坐标原点)。
的一个焦点的直线交椭圆于A、B两点,求△AOB的面积的最大值(O为坐标原点)。
9.已知椭圆![]() (a>b>0),它的一条准线方程是x=1,倾斜角为45°的直线交椭圆于A、B两点,设AB的中点为M,直线AB与OM的夹角为α
(a>b>0),它的一条准线方程是x=1,倾斜角为45°的直线交椭圆于A、B两点,设AB的中点为M,直线AB与OM的夹角为α
(1)当tanα=2时,求椭圆的方程;
(2)当2<tanα<3时,证明![]() 。
。
10.设椭圆的方程为![]() (m>0,n>0),过原点且倾斜角为θ和π-θ
(m>0,n>0),过原点且倾斜角为θ和π-θ![]() 两条直线分别交椭圆于A、C和B、D四点
两条直线分别交椭圆于A、C和B、D四点
(1)用θ、m、n表示四边形ABCD的面积S;
(2)若m、n为定值,当θ在![]() 上变化时,求S的最大值u;
上变化时,求S的最大值u;
(3)如果u>mn,求![]() 的取值范围。
的取值范围。
答案与提示
一、1.D
2.A
3.B
4.C
5.C
二、6.![]()
7.6π
三、8.提示:由题意椭圆焦点为(0,±1),设直线AB过焦点F(0,1),其方程为:y-1=kx,代入![]() 得
得![]() ,设
,设![]() ,
,![]() ,则
,则![]() 、
、![]() 为该方程的两根,由
为该方程的两根,由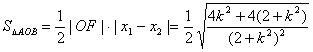
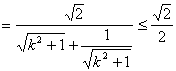 (当且仅当k=0时取等号),可知△AOB面积的最大值为
(当且仅当k=0时取等号),可知△AOB面积的最大值为![]()
9.提示:(1)由![]() 得
得![]() ,又
,又![]()
∴椭圆方程为![]() 将AB的方程y=x+m代入整理得
将AB的方程y=x+m代入整理得![]()
∴![]()
于是![]() ,由
,由![]() ,得
,得![]() 或c=--2(舍),于是所求椭圆方程为
或c=--2(舍),于是所求椭圆方程为![]()
(2)由(1)![]() ,又
,又![]() ,得
,得![]()
∴![]() ,
,![]() 即
即![]()
10.提示:(1)设过原点倾斜角为θ的直线的方程为y=xtanθ,可得方程组
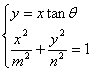
又由对称性,得四边形ABCD为矩形,同时![]() ,所以四边形ABCD的面积
,所以四边形ABCD的面积![]()
(2)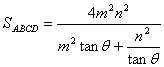 。考虑函数
。考虑函数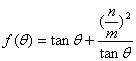 在
在![]() 的单调性。易证明
的单调性。易证明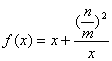 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,因此有:
上是增函数,因此有:
当m>n时,![]() ,此时
,此时![]() ,u=2mn
,u=2mn
当m<n时,![]()
∴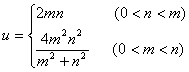
(3)当![]() 时,u=2mn>mn恒成立
时,u=2mn>mn恒成立
当![]() 时,
时,![]() ,即有
,即有![]() ,解得
,解得![]() ,又
,又![]() ,故
,故![]()