椭圆及其标准方程练习
一、选择题（每小题四个选项中，只有一项符合题目要求）
1．设椭圆
的两焦点为
、
，点P在椭圆上，若线段
的中点Q恰好在y轴上，那么
是
的（ ）
A．7倍
B．5倍
C．4倍
D．3倍
2．设b≥2a>0，则曲线
上对两焦点张角为直角的点有（ ）
A．0个
B．0个或2个
C．2 个或4个
D．0个或2个或4个
3．点P在椭圆
上，则点P到直线3x-2y-16=0的距离的最大值是（ ）
A．
B．
C．
D．
4．设椭圆
的两个焦点分别为和，P为椭圆上一点，并且
，则
等于（ ）
A．
B．
C．
D．
5．过点M（-2，0）的直线l与椭圆
交于
、
两点，线段
的中点为P，设直线l的斜率为
，直线OP的斜率为
，则
的值为（ ）
A．2
B．-2
C．
D．
6．方程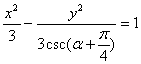
表示椭圆时，α适合的条件是（ ）
A．
B．
C．
D．
二、填空题
7．△ABC中，三边a、c、b成等差数列，且a>c>b，若A（-1，0），B（1，0），则动点C的轨迹方程为____________。
8．以（1，0），（3，0）为焦点且经过原点的椭圆的方程为__________。
三、解答题
9．过椭圆
内一点D（1，0）引动弦AB，求弦AB的中点M的轨迹方程。
10．椭圆
上有两点P、Q，O是原点，若OP、OQ斜率之积为
。求证
为定值。
11．已知点A在圆C：
上运动，点B在以
为右焦点的椭圆
上运动，求AB的最大值。
答案与提示
一、1．A 2．C 3．C 4．B 5．D 6．C
二、7．
8．
三、9．提示：设
，
，AB的中点M（x，y），则
，
，且
① 
②，①-②得
∴
又
∴
即所求的轨迹方程为
10．提示：设直线OP的方程为y=kx，则直线OQ的方程为
由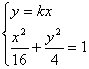
得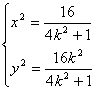
∴
同理可求得
∴
11．提示：如图8-1所示
∵
∴k=4
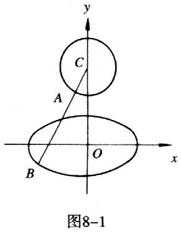
∴椭圆的方程为
。AB的最大值是椭圆
上动点B（x，y）到圆C的圆心（0，2）距离的最大值与圆的半径之和。设B（x，y）到（0，2）的距离为d，则由两点的距离公式有
。又B（x，y）在椭圆上
∴
。
因为B（x，y）是椭圆上的点
∴-1≤y≤1
∴当
时，
最大为
∴