空间向量及其运算2

空间向量及其运算2

一、知识回顾：

1、  向量的概念及运算，共线向量、共面向量概念，共线向量定理、共面向量定理；

2、  空间向量基本定理及推论；

3、  向量数量积的概念、性质、计算方法、运算律和主要用途。

二、基础练习：

1、已知平行六面体ABCD-EFGH，则在向量，，，，，，中，共线的向量有　　　　　　　　　　　　　 ，共面的向量有　　　　　　　　　　　　 。

2、在空间四边形ABCD中，给出下列四个等式，其中成立的等式序号有　　　　 　　　

①②③④。

3、在空间四边形ABCD中，如果G、H分别是△ABC、△OBC的重心，设，，，则向量可用、、表示为　　　　  　　　　　　。

4、在下列条件中，能使M与A、B、C共面的条件是（　　）
A.　　B.
C.　　　 D.

5、设{、、}是空间的一个基底，若存在实数、、，使得，
则必有　　　　　　　 。

6、已知向量、之间的夹角为，且，，则　　 　 。

三、例题讲解：

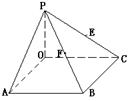
1、四棱锥P-OABC的底面为一矩形，平面OABC，设，，，E、F分别是PC和PB的中点，用、、表示：、、、。

2、  在空间四边形ABCD中，如果，求证：

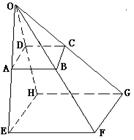3、已知平行四边形ABCD，从平面AC外一点O引向量，， ，，
求证：（1）四点E、F、G、H共面；（2）平面EG∥平面AC

4、已知平行六面体ABCD-A₁B₁C₁D₁，底面ABCD是边长为1的正方形，侧棱AA₁=2，并且AA₁与AB、AD的夹角均为，
（1）求线段AC₁的长；
（2）若K为BC₁的中点，求AK的长；
（3）求异面直线BD₁和AC所成角的大小。

四、巩固练习：

1、设{、、}是空间的一个基底，则下列各选项中能构成基底的一组向量是（　 ）
A. ，-2，+ B. +，-， C. 2+2，+，2 D. +，+，++2

2、在△ABC中，E、F、D分别是边AC、AB、BC的中点，则=　　 　 　。

3、对空间任一点O和不共线的三点A、B、C，若向量，
且A、B、C、D四点共面，则实数k=　　　　　　　　　　。

4、已知向量、、满足++，，，，则++=　

5、正四棱锥P-ABCD中，O是底面中心，Q是CD的中点，求下列各题中的x，y值：
（1）（2）

6、已知平行四边形ABCD中，AB=AC=1，，将它沿对角线AC折起，使AB和CD所在直线成角，求此时B、D两点的距离。

7、在空间四边形PABC中，已知PA、PB、PC两两互相垂直，O为P在△ABC内的射影，试用向量证明O为△ABC的垂心。