空间直线

　　　　　  高二数学期末复习讲义（2）　　

空间直线

一．复习目标：

1．了解空间两条直线的位置关系．

2．掌握两条直线所成的角和距离的概念，会计算给出的异面直线的公垂线段的长．

二、基础知识；

1、目前所学过的证明线线平行的方法有：（用符号表示）

（1）公理4：

（2）线面平行线线平行：

（3）垂直同一平面线线平行：

2、目前所学过的证明线线垂直的方法有：（用符号表示）

（1）线垂直面：

（2）三垂线定理及逆定理：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

（3）勾股定理的逆定理：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

（4）异面直线夹角：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

3、异面直线的判定定理：　　　

　 异面直线的证明常用方法：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

4、异面直线所成的角（1）范围：　　　　　　　　　 　　　　　 

　 （2）怎样找角：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

（３）等角定理：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

５、异面直线的公垂线确定的方法：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿　　　　　　　　　　　　　　　　　  　　　

三．课前预习：

1．下列四个命题：

（1）分别在两个平面内的两条直线是异面直线

（2）和两条异面直线都垂直的直线有且只有一条

（3）和两条异面直线都相交的两条直线必异面

（4）若与是异面直线，与是异面直线，则与也异面

其中真命题个数为　　　（ 　　 ）

3　　　　 2　　　　 1　　　　 0

2．在正方体中，、分别是棱和的中点，为上底面的中心，则直线与所成的角为（　 　　 ）

30⁰  45⁰ 60⁰ 

3．在棱长为的正四面体中，相对两条棱间的距离为________________．

4．两条异面直线、间的距离是1cm，它们所成的角为60⁰，、上各有一点A、B，距公垂线的垂足都是10cm，则A、B两点间的距离为____________________．

三．例题分析：

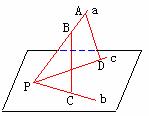例1．已知不共面的三条直线、、相交于点，，，，，求证：与是异面直线．

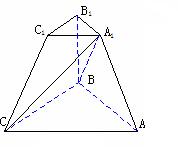例2．在三棱台中，侧棱⊥底面，且，．

（1）求证：，，．

（2）求异面直线和的距离．

小结：

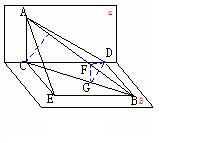例3． 一条长为的线段夹在互相垂直的两个平面、之间，AB与所成角为，与所成角为，且，，，、是垂足，求（1）的长；（2）与所成的角

解：

四．课后作业：　　　　　　　　　　　　　 班级　　　学号　 　 姓名　　　　　　

1．AB、CD在平面α内，AB//CD，且AB与CD相距28厘米，EF在平面α外，EF//AB，且EF与AB相距17厘米，EF与平面α相距15厘米，则EF与CD的距离为（　　　 ）

25厘米　　  39厘米　　　 25或39厘米　　15厘米

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　

2．已知直线a，如果直线b同时满足条件：①a、b异面②a、b所成的角为定值③a、b

间的距离为定值，则这样的直线b有（　　　　　）

1条　　　　 2条　　　　  4条　　　　　  无数条

3．已知异面直线a与b所成的角为50⁰，P为空间一点，则过点P与a、b所成的角都是30⁰的直线有且仅有（ 　　　　　 ）

1条　　　　2条　　　　  3条　　　　　  4条

4．在正三棱柱中，若，则与所成的角的大小　　 ．　

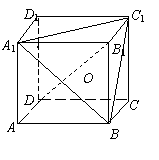5．如图，在正方体ABCD－A₁B₁C₁D₁的中，求证：B₁D被平面A₁BC₁分成1∶2的两段．

证明：

6．如图，已知平面α、β交于直线，AB、CD分别在平面α，β内，且与分别交于B，D两点．若∠ABD＝∠CDB，试问AB，CD能否平行？并说明理由．

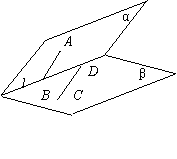证明：

 

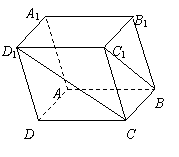7．平行六面体ABCD－A₁B₁C₁D₁中，求证：CD₁所在的直线与BC₁所在的直线是异面直线．

证明：