命题，圆锥曲线，空间向量

第一学期仲元高二数学测试(4)（命题，圆锥曲线，空间向量）

一、选择题

1.下列语句是命题的为　　　　　　　　　　　　　　　　　　　　　　　 

A. x-1=0　　B. 他还年青　　 C. 20-5×3=10　　  D. 在20020年前,将有人登上为星

2.命题 “若△ABC不是等腰三角形,则它的任何两个内角不相等”的逆否命题是　

A.　　  “若△ABC是等腰三角形,则它的任何两个内角相等”　

B.　　  B “若△ABC任何两个内角不相等,则它不是等腰三角形”

C  “若△ABC有两个内角相等,则它是等腰三角形”　

D “若△ABC任何两个角相等,则它是等腰三角形”

4. 给出下列三个命题

①若,则

②若正整数m和n满足,则

③设为圆上任一点，圆O₂以为圆心且半径为1.当时,圆O₁与圆O₂相切

其中假命题的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 A．0 　　　　　　　　　　　B．1 　　　　　　　　　　　 C．2　　　　　　　　　　　 D．3

5．双曲线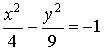的渐近线方程是　　　　　　　　　　 

　　　 A．　　　　　B．　　　　 C．　　　　　 D．

6. 已知M(-2,0),N(2,0),PM-PN=4,则动点P的轨迹是

A.双曲线　 B.双曲线左支　 C.一条射线　 D.双曲线右支

7.如果方程x²+ky²=2表示焦点在y轴上的椭圆,那么实数k的取值范围是

A. (0,+∞)　　 B. (0,2)　　　 C. (1,+∞) 　　 D. (0,1)

8.已知向量与向量平行,则x,y的值分别是　

　A. 6和-10　　　B. –6和10　　 C. –6和-10　　　 D. 6和10

9.已知ABCD是平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),则顶点D的坐标为　

　A. (1,1,-7)　　　B. (5,3,1)　　　　 C. (-3,1,5)　　　　　 D. (5,13,-3)

10. 方程表示的曲线为　

 A. 抛物线　　　B. 椭圆　　　C. 双曲线　　 D.圆

二、填空题

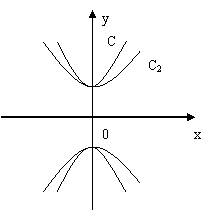
11. 右图中两个两条双曲线的离心率分别是、，

且，则曲线的离心率是___ __，

曲线的离心率是___ __.

12.直线l过抛物线y²=a(x+1)(a>0)的焦点,并且与x轴垂直,

若l被抛物线截得的线段长为4,则a=　　　　　　　　 .

13.已知下列命题(是非零向量)

(1)若,则; (2)若,则;

(3)

 则假命题的个数为___________

14. 已知向量，且A、B、C三点共线，

则k=　　　　　　  .

三、解答题

15.如果正△ABC中,D∈AB,E∈AC,向量,求以B,C为焦点且过点D,E的双曲线的离心率.

16. 如图,在正方体ABCD-A₁B₁C₁D₁中,E、F分别是BB₁、CD的中点.

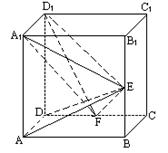(Ⅰ)证明AD⊥D₁F;(Ⅱ)求AE与D₁F所成的角;(Ⅲ)证明面AED⊥面A₁FD₁;

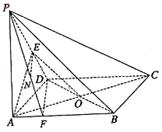
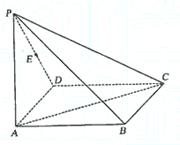
17. 如图，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点.

　 （Ⅰ）求直线AC与PB所成角的余弦值；

（Ⅱ）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离.

18. 设0<a,b,c<1,用反证法证明: (1-a)b,(1-b)c,(1-c)a不同时大于

19.已知p：l-≤2；q：x²-2x+l—m²≤0(m>0)，若¬p是¬q的必要而不充分条件，求实数m的取值范围．

20. 已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为。

　　(1) 求双曲线C的方程；

(2) 若直线l：与双曲线C恒有两个不同的交点A和B，且(其中O为原点)，求k的取值范围。

第一学期仲元高二数学测试(4)参考答案

一.　 选择题　CCBBA　CDADA

二.　 填空题

11. e₁, e₂;  12. 4;　　13. 3;　　14.

三.　 解答题

15. 解:

16. (Ⅰ)

　 ∴AD⊥D₁F

(Ⅱ)

　∴AE⊥D₁F

　AE与D₁F所成的角为90⁰

(Ⅲ)由以上可知D₁F⊥平面AED

　 ∴面AED⊥面A₁FD₁;

17．解法1：（Ⅰ）建立如图所示的空间直角坐标系，

则A、B、C、D、P、E的坐标为A（0，0，0）、

B（，0，0）、C（，1，0）、D（0，1，0）、

P（0，0，2）、E（0，，1），

从而

设的夹角为θ，则

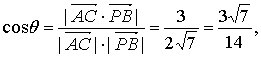
∴AC与PB所成角的余弦值为.

 （Ⅱ）由于N点在侧面PAB内，故可设N点坐标为（x，O，z），则，由NE⊥面PAC可得，

　∴

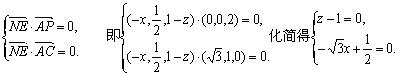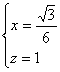
即N点的坐标为，从而N点到AB、AP的距离分别为1，.

解法2：几何法,略

18. 证明:假设结论不成立,即(1-a)b,(1-b)c,(1-c)a都大于

∴(1-a)b (1-b)c (1-c)a>　　　　(1)

而

(1-a)b (1-b)c (1-c)a 与(1)式矛盾,假设不成立

故(1-a)b,(1-b)c,(1-c)a不同时大于

19. 解：（1）设点M(x,y)是曲线上任意一点,则-x=1，

 化简得:y²=2x+2x

所求曲线的方程. C₁：当x³0时， y²=4x；C₂：当x<0时，y=0.　

（2）直线y=kx+1过定点(0,1)，

y=kx+1，与y²=4x联列：ky²-4y+4=0, D=16-16k

当k=0时,直线与C₁有一个公共点,而与C₂没有公共点,共1个公共点;

当k=1时, D=0，直线与C₁和C₂各一个公共点,共2个公共点;

当0<k<1时，D>0,直线与C₁有2个公共点，和C₂一个交点,共3个公共点;

当k<0时，D>0,直线与C₁有两个公共点，和C₂没有公共点,共2个公共点;

当k>1时, D<0,直线与C₁没有公共点，和C₂有1个公共点,共1个公共点;

 所以:当k=0,或k>1时,直线与曲线有1个公共点;

当k=1,或k<0时,直线与曲线有2个公共点;

当0<k<1时,直线与曲线有3个公共点.

20.解：（Ⅰ）设双曲线方程为　

由已知得

故双曲线C的方程为

（Ⅱ）将

由直线l与双曲线交于不同的两点得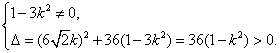

即　①　设，则

而

于是　　②

由①、②得　

故k的取值范围为