抛物线的简单几何性质练习
一、选择题（每小题四个选项中，只有一项符合题目要求）
1．如果抛物线的顶点在原点，对称轴为x轴，焦点在直线3x-4y-12 =0 上，则抛物线的方程是（ ）
A．
B．
C．
D．
2．AB是抛物线
的一条过焦点的弦，AB=20，AD、BC垂直于y轴，D、C分别为垂足，则梯形ABCD的中位线长是（ ）
A．5
B．
C．
D．10
3．以
的中心为顶点，以左准线为准线的抛物线与椭圆的右准线交于A、B两点，则AB的值为（ ）
A．
B．
C．
D．
4．设抛物线的顶点在原点，其焦点F在y轴上，又抛物线上的点（k，-2）与F点的距离为4，则k等于（ ）
A．4
B．4或-4
C．-2
D．-2或2
5．过抛物线
的焦点作直线交抛物线于
、
两点，如果
，那么AB等于（ ）
A．10
B．8
C．6
D．4
6．p是抛物线
上一点，p到点
的距离为
，p到直线
的距离为
，当
取最小值时，点p的坐标为（ ）
A．（0，0）
B．（2，2）
C．
D．
二、填空题
7．已知F是抛物线的焦点，M是这抛物线上的一个动点，P（3，1）是一个定点，则MP+MF的最小值是_________。
8．有一个正三角形的两个顶点在抛物线
上，另一个顶点在原点，则这个三角形的边长是_______。
三、解答题
9．已知点A（5，0）和抛物线上的动点P，点M分线段PA为PM：MA=3：1，求点M的轨迹方程。
10．过抛物线
的焦点，引倾斜角为120°的直线，交抛物线于A、B两点，求△OAB的面积。
11．试求点P（0，a）（a>1）到曲线
上点的最短距离。
答案与提示
一、1．C 2．B 3．D 4．B 5．B 6．B
二、7．4 8．12
三、9．提示：设M（x，y），
∵PM：MA=3：1
∴
，
即
，
，又点P在抛物线上
∴
∴
即所求点M的轨迹方程为
10．提示：由得p=2，焦点（-1，0），直线
由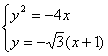
得
，易求得
∴△AOB的面积
11．提示：（1）当
，即
时，
，由图像可知P（0，a）在这条抛物线顶点A（0，1）的正上方，故PA=a-1为最短距离
（2）当
，即
或
时，
，设抛物线上任意一点
，则
∵2a>2 
，则
可以取到2a，故当
时，
∴
（3）比较a-1与
的大小。由
①若a（a-4）<0即0<a<4，又a>1
∴1<a<4时，有
∴最短距离为a-1
②若a（a-4）>0，即a >4时，
，最短距离为
③若a（a-4）=0，即a=4时，最短距离为3
综上所述：a=4时，最短距离为3，
1<a<4时，最短距离为a-1，
a>4时，最短距离为