高二数学下学期期末专题复习
12：平面的基本性质
【知识网络】
【学法点拨】
1．必须明确本章内容的复习目标：
（1）准确理解和系统掌握空间直线和平面的各种位置关系（特别是平行与垂直的位置关系），能够运用概念、公理、定理等进行严密的推理判断和逻辑论证；
（2）正确理解空间的各种角和距离的概念，能将其转化为平面角和线段的长度，并能熟练地运用平面几何及三角知识来计算；
（3）通过图形能迅速判断几何元素的位置关系，能熟练绘制符合要求的空间图形的直观图、截面图，熟练地处理折叠、截面的问题. 但要注意立体几何中的示意图不反映元素关系的真实结构，逻辑论证仍是关键；
（4）理解用反证法证明命题的思路，会证一些简单的问题.
2．要掌握解题的通法，推理严谨，书写规范
（1）转化法是空间直线和平面的位置关系的判断与证明的常用方法，线线关系（主要指平行和垂直）、线面关系、面面关系三者中，每两者都存在着依存关系，充分、合理地运用这些关系是解题的关键；另外，转化法还常常运用在求距离时点的位置的变化，以及线面距、面面距间的转化；
（2）求角或距离的步骤是“一作、二证、三计算”，即先作出所求角或表示距离的线段，再证明它就是所要求的角或距离，然后再进行计算，尤其不能忽视第二步的证明.
【考点指津】
掌握平面基本性质的三条公理及公理3的三条推论，能运用它们证明空间的共点、共线、共面问题.
【知识在线】
1． 如果
那么下列关系成立的是
( )
A．
B．
C．
D．
2． 下列四种说法：
(1) 两个平面可以仅有一个公共点；
(2) 空间任意四边形一定是平面图形；
(3) 三条互相平行的直线最多可确定三个平面；
(4) 有三个不同公共点的两个平面一定重合．
其中正确的个数是 ( )
A．0
B．
3． 一条直线和直线外四个不同的点，它们最多能确定平面的个数是 ( )
A．6
B．
4．在空间四边形
各边
、
、
、
上分别取
、
、
、
四点，如果
，则有
( )
A．
B．
C．或
D．
或
【讲练平台】
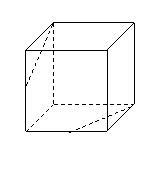
例1 如图9-1，在正方体
中，
为的中点，为
的中点．
求证：(1)
四点共面；
(2) 
三线共点．
分析 要证四点共面，可由这四点连成两条直线，证明它们平行或相交即可；对于（2）中证三线共点，可证两条直线的交点在第三条直线上．
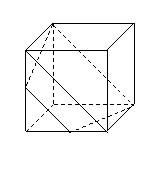证明 (1) 如图9-2，分别连结
分别是和的中点，
．
又
，
是平行四边形．
， 从而
∥．
根据推论3，和确定一个平面，故四点共面．
(2)
， ，
∴．∴直线
和
必相交．
令
．
平面
，
平面．
同理
平面
．
即
是平面和平面的公共点，
而平面
平面=
，
故三线共点．
点评 1．本题也可先证明与相交，与相交，且交点重合，从而证得(2)，既然与相交，那么(1)自然就成立了．
2．证明四点共面的主要方法是四点连成两条直线，证明它们平行或相交．
3．证明三线
共点的主要方法有：①证明
与
相交，与
相交，再证交点重合；②先证与相交于点，再证
．
例2 已知四条直线
两两相交，但不共点，求证：共面．
分析 四线不共点，三线有可能共点，也可能无三线共点，因而要分类讨论!
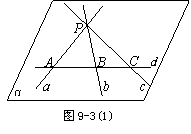
证明 ① 如图9-3(1)，设都经过点． 则由条件知此时
．
于是根据推论1，经过点与直线
存在一个平面，设该平面为
．
与相交，设交点为
，
不是同一点，
．
同理 
所以共面．
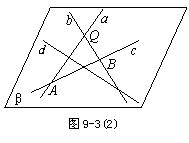
② 如图9-3(2)，设无三条直线共点，由已知
相交，设交点为
，根据推论2，经过存在一个平面，设该平面为
．
与
相交，与相交，且不经过点， 
与交于不同两点A，B，即与平面有两个不同的公共点， 
． 同理
．所以都在平面内，故共面．
点评 证明共面问题的主要方法有：①先由公理3或其推论证明某些元素确定一个平面，再证其余元素都在此平面内； ② 指出给定的元素中的某些元素在平面内，某些元素(与前述元素有公共元素，但两部分必须包括所有元素)在平面内，再通过公共元素来证明与重合．如“若一直线与三条平行直线都相交，则这四条直线共面”的证明就用此法．
以上两例归纳了共线、共点、共面问题的证明思路。
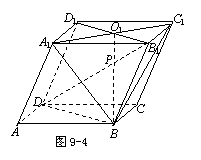例3 如图9-4，平行六面体中， 
平面
求证：
(1) 
；
(2) 
被平面
截于三等分点．
分析 （1） 要证点P在直线BO1上， 可考虑两个相交平面，
使点P为这两个平面的公共点，而BO1为这两个平面的交线．
（2）会用点、线、面去思维。
简证 (1) 因为点既在平面
内，又在平面内，
所以点必在它们的交线
上． 从而．
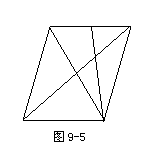
(2) 将对角面
移出(如图9-5)，连
（评：多余。其实由
即得结论），
则是△B1D1B的重心．
即被平面截于三等分点．
点评 将对角面从线条复杂的平行六面体中移出，既使问题简单化，又将图形“恢复”其本来面目（平面图形）．
分解和移动图形，“降维”等都是处理立体几何问题的重要思想方法．
【知能集成】
本课的主要内容是平面的基本性质，它是研究立体几何的理论基础．
注意以下几点：
1．会用图形语言、文字语言和符号语言准确描述三个公理（推论）；理解它们的基本应用（如例1，例2）．
2．处理立体几何问题的基本思想是“降维”，把较为复杂的问题化归为平面几何问题（如例3）．要充分利用平面几何中的基本图形解决问题．
【训练反馈】
1． 下列判断正确的是 ( )
A．两条直线确定一个平面
B．如果平面和有三个公共点，则与重合
C．有一个公共点的两个平面交于过这一点的一条直线
D．点
且与平面有公共点，则点在平面内
2． 可使平面和重合的条件是它们的公共部分中有
( )
A．三个点 B．一个点和一条直线
C．无数个点 D．两条不重合，不异面的直线
3．
两条相交直线
都在平面内且都不在平面内． 命题甲：
和
中至少有一条与相交； 命题乙：平面和相交，则甲是乙的
( )
A．充分但不必要条件 B．必要但不充分条件
C．充分且必要条件 D．既非充分也非必要条件
4． 用适当的符号填空：若
则 ．
5． 不重合的三条直线，若相交于一点，则最多能确定 个平面； 若共有两个交点，最多能确定 个平面； 若共有三个交点，最多能确定 个平面．
6．
已知直线与三条平行直线都相交，求证：这四条直线共面．
7． 三个平面两两相交于三条直线，若这三条交线不互相平行，：求证它们必交于一点．
8． 已知△ABC的三个顶点都不在平面内，它的三边
延长后分别交平面于
．求证： 在同一条直线上．
答案
【知识在线】
1．A 2．B 3．C 4．B
【训练反馈】
1．C 2．D 3．C 4．
5．3，2，1 6．先由确定一个平面，证、
； 同理可证
共面于平面．由
确定一个平面知
重合． 7．设
，
．由
得
． 于是
8．设法证明是平面
和平面的公共点．