高中学生学科素质训练
高二数学同步测试（12）—圆锥曲线
一、选择题（本大题共10小题，每小题5分，共50分）
1．
所表示的曲线是 （ ）
A．双曲线 B．椭圆
C．双曲线的一部分 D．椭圆的一部分
2．椭圆短轴长是2，长轴是短轴的2倍，则椭圆中心到准线距离是 （ ）
A．
B．
C．
D．
3．已知椭圆
上一点P到椭圆一个焦点的距离为3，则P到另一个焦点的距离为
（ ）
A．2 B．
4．连接双曲线
与
的四个顶点构成的四边形的面积为S1，连接它们的的四个焦点构成的四边形的面积为S2，则S1：S2的最大值是 （ ）
A．2 B． 
D．
5．与椭圆
共焦点，且两准线间的距离为
的双曲线方程为 （ ）
A．
B．
C．
D．
6．设k>1，则关于x，y的方程(1-k) x2+ y 2=k2-1所表示的曲线是 （ ）
A．长轴在y轴上的椭圆 B．长轴在x轴上的椭圆
C．实轴在y轴上的双曲线 D．实轴在x轴上的双曲线
7．双曲线
的两条渐近线互相垂直，那么该双曲线的离心率是 （ ）
A．2 B．
C．
D．
8．动点P到直线x+4=0的距离减去它到M（2，0）的距离之差等于2，则点P的轨迹是（ ）
A．直线 B．椭圆 C．双曲线 D．抛物线
9．抛物线y =-x2 的焦点坐标为 （ ）
A．(0, ) B． (0, -) C．(, 0) D． (-, 0)
10．过抛物线
的焦点F作倾斜角为
的弦AB，则AB的值为 （ ）
A．
B．
C．
D．
二、填空题（本大题共4小题，每小题6分，共24分）
11．椭圆
的一个焦点坐标是（0，1），则m=
．
12．双曲线x2-
=1截直线y =x+1所得弦长是 ．
13．已知抛物线y2=2x，则抛物线上的点P到直线l：x-y+4=0的最小距离是 ．
14．已知直线x- y =2与抛物线交于A、B两点，那么线段AB的中点坐标是 ．
三、解答题（本大题共6小题，共76分）
15．求两焦点的坐标分别为（-2，0），（2，0），且经过点P（2，
）的椭圆方程．（12分）
16．已知抛物线C的准线为x =
（p>0），顶点在原点，抛物线C与直线l:y
=x-1相交所得弦的长为3
，求
的值和抛物线方程．（12分）
17．已知椭圆：
上的两点A（0，
）和点B，若以AB为边作正△ABC，当B变动时，计算△ABC的最大面积及其条件．（12分）
|
18．已知双曲线经过点M（
），且以直线x= 1为右准线．
（1）如果F（3，0）为此双曲线的右焦点，求双曲线方程；
（2）如果离心率e=2，求双曲线方程．（12分）
19．设F1，F2为椭圆
的两个焦点，P为椭圆上的一点，已知P、F1、F2是一个直角三角形的三个顶点，且
的值．（14分）
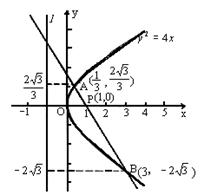
20．已知动圆过定点P（1，0），且与定直线
相切，点C在l上．
（Ⅰ）求动圆圆心的轨迹M的方程；
（Ⅱ）设过点P，且斜率为－的直线与曲线M相交于A、B两点．
（i）问：△ABC能否为正三角形？若能，求点C的坐标；若不能，说明理由；
（ii）当△ABC为钝角三角形时，求这种点C的纵坐标的取值范围． （14分）
参考答案（12）
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | D | D | C | A | C | C | D | B | B |
二．填空题（本大题共4小题，每小题6分，共24分）
11．3 12．
13．
14．（4，2）
三、解答题（本大题共6题，共76分）
15．（12分）[解析]：由题意可知，c=2，设椭圆方程为
，则
①
又点P（2，）在椭圆上，所以
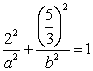②，
联立①②解得，
或
（舍去），
故所求椭圆方程是
16．（12分）[解析]：由题意，可设C的方程为
，C与直线l:y
=x-1相交于A、B两点，
由此可得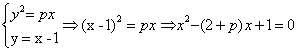
，
所以，
= 
=
= 
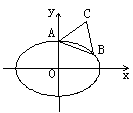因为p>0，所以解得
，
故抛物线方程为
．
17．（12分）[解析]：由题意可设B（2cosθ, sinθ），
则
因为S△ABC=
·
=·
=·
所以当
=-1时，即B点移动到（0，-）时，△ABC的面积最大，且最大值为3．
18．（12分）[解析]：（1）设P（x，y）为所求曲线上任意一点，由双曲线定义得
=
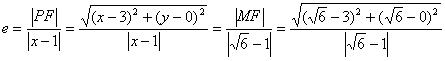化简整理得
（2）
因此，不妨设双曲线方程为
，
因为点M（）在双曲线上，所以
，得
，
故所求双曲线方程为
19．（14分）[解析]：由已知得
． 根据直角的不同位置，分两种情况
若
解得
若
解得
．
20．（14分）[解析]：（Ⅰ）依题意，曲线M是以点P为焦点，直线l为准线的抛物线，
所以曲线M的方程为
．
（Ⅱ）（i）由题意得，直线AB的方程为
消y得
所以A点坐标为
，B点坐标为（3，
），
|
则BC=AB且AC=AB，即
|
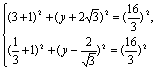
由①－②得
但
不符合①，所以由①，②组成的方程组无解．
因此，直线l上不存在点C，使得△ABC是正三角形．
（ii）解法一：
设C（－1，y）使△ABC成钝角三角形，由
，
即当点C的坐标为（－1，
）时，A，B，C三点共线，故
．
又
，
， 
．
当
，即
，
即
为钝角．
当
，即
，
即
为钝角．
又
，即
，
即
． 该不等式无解，所以∠ACB不可能为钝角．
因此，当△ABC为钝角三角形时，点C的纵坐标y的取值范围是
．
解法二：
以AB为直径的圆的方程为
．
圆心
到直线的距离为，
所以，以AB为直径的圆与直线l相切于点G
．
当直线l上的C点与G重合时，∠ACB为直角，当C与G
点不重合，且A，B，C三点不共线时， ∠ACB为锐角，即△ABC中∠ACB不可能是钝角．
因此，要使△ABC为钝角三角形，只可能是∠CAB或∠CBA为钝角．
过点A且与AB垂直的直线方程为
．
过点B且与AB垂直的直线方程为
． 令
．
又由
，所以，当点C的坐标为（－1，）时，A，B，C三点共 线，不构成三角形．
因此，当△ABC为钝角三角形时，点C的纵y的取值范围是