高中学生学科素质训练
高二数学同步测试—简单几何体（4）
一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若正棱锥的底面边长与侧棱长都相等，则该棱锥一定不是 （ ）
A．三棱锥 B．四棱锥 C．五棱锥 D．六棱锥
2．一个棱柱是正四棱柱的条件是 （ ）
A．底面是正方形，有两个侧面是矩形
B．底面是正方形，有两个侧面垂直于底面
C．底面是菱形，且有一个顶点处的三条棱两两垂直
D．每个侧面都是全等矩形的四棱柱
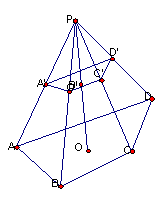
3．如图，棱锥P-ABCD的高PO＝3，截面积A’B’C’D’平行于底面ABCD，PO与截面交于O’，且OO’＝2。如果四边形ABCD的面积为36，则四边形A’B’C’D’的面积为 （ ）
A．12 B．
4．一个凸多面体的面数为8，各面多边形的内角总和为16π，则它的棱数为 （ ）
A．24 B．
5．在棱长为1的正方体AC1中，对角线AC1在六个面上的射影长度总和是 （ ）
A．
B． 
C．6 D．
6．若一个四面体由长度为1，2，3的三种棱所构成，则这样的四面体的个数是 （ ）
A．2 B．
7．棱长为a的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为（ ）
A．
B．
C．
D．
8．已知一个简单多面体的每个面均为五边形，且它共有30条棱，则此多面体的面数F和顶
点数V分别等于 （ ）
A．F=6,V=26 B．F=8,V=24
C．F=12,V=20 D．F=20,V=12
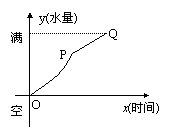
9．有一空容器，由悬在它上方的一根水管均匀地注水，直至
把容器注满。在注水过程中水面的高度曲线如右图所示，
其中PQ为一线段，则与此图相对应的容器的形状是（ ）
 |  |  | |||||
 | |||||||
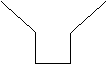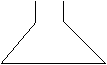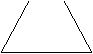A． B． C． D．
10．一个水平放置的圆柱形贮油桶，桶内有油部分占底面一头的圆周长的
，则油桶直立时，油的高度与桶的高之比是 （ ）
A． B．
C．
D．
11．平行六面体ABCD-A´B´C´D´的六个面都是菱形，那么顶点B在平面ACB´上的射影一定是⊿ACB´的
A．重心 B． 外心 C．内心 D．垂心
12．棱长为a的正四面体中，高为H，斜高为h，相对棱间的距离为d，则a．H．h．d的大
小关系正确的是 （ ）
A．
B．
C．
D．
二、填空题：本大题满分16分，每小题4分，各题只要求直接写出结果．
13．正方体
中，棱长为a，E是
的中点，在对角面
上取一点M，使AM+ME最小，其最小值为
.
14．一个三棱锥的三个侧面中有两个是等腰直角三角形，另一个是边长为1的正三角形，这样的三棱锥体积为 （写出一个可能值）．
15．在正四棱锥P—ABCD中，若侧面与底面所成二面角的大小为60°，则异面直线PA与BC所成角的大小等于 ．（结果用反三角函数值表示）
16．如图，在直四棱柱A1B
三、解答题：本大题满分74分．
17．（10分）已知三棱锥的底面是边长为1的正三角形,两条侧棱长为
, 试求第三条侧棱长的取值范围．
18．（12分）今年庄稼丰收，这些粮食往哪儿放呢？东东爹想了个好办法：拿一块长方形木板，借助两面墙，在偏屋的墙角处围一个直三棱柱的谷仓。而木板可以立着放，可以横着放，怎样放装粮食多呢？
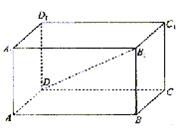19．（12分）长方体的底面积是4，对角线长是4，求长方体侧面积的最大值
20．（12分）
已知简单多面体的顶点数．面数．数分别为V．F． E． 多面体的各面为正x边形，过同一顶点的面数为y． 求证：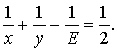 
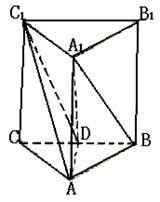
21．（14分）如图，正三棱柱ABC—A1B
|
（Ⅱ）求点D到平面ACC1的距离；
（Ⅲ）判断A1B与平面ADC的位置关系，
并证明你的结论
22．（14分）如图，在三棱锥
中，
平面
，
，
，D为BC的中点．
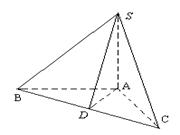（1）判断AD与SB能否垂直，并说明理由；
（2）若三棱锥的体积为
，且
为
钝角，求二面角
的平面角的正切值；
（3）在（Ⅱ）的条件下，求点A到平面SBC的距离．
（四）
一、选择题：（每小题5分，共60分）
1．D 2．C 3．C 4．D 5．B 6．A 7．C 8．C 9．C 10．B 11．B 12．B
6．满足条件的四面体只有如下两种情形：
 |
7．解：该内接正八面体的棱长为
，
它的体积为
选C
10． 设圆柱的底面半径为R，高为h，油桶直立时油面的高度为x，则
选B．
11．解：∵BA=BC=BB´,∴B在平面ACB´上的射影到三个顶点的距离也相等，即射影为⊿ACB´的外心。答案：B。
12． 易得
∴ .选B．
二、填空题：本大题满分16分，每小题4分
13．
14．
15．
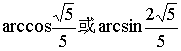16．AC⊥BD,或AB=AD且BC=DC
13．解：
设AC∩BD=O，则AO=CO． ∴平面是线段AC的垂直平分面，∴C是A关于平面的对称点。连CE交面于M ，则M 就是要求的点，这时AM+ME 最小。又AM=CM, ∴AM+ME的最小值就是CE 的长，而
=, ∴AM+ME的最小值为．
三、解答题：本大题满分74分．
17． 解: 如图, 四面体ABCD中,AB=BC=CA=1（2分）, DA=DC=（4分）, 只有棱DB的长x是可变的． 在三角形ACD中, M为AC的中点, MD=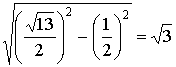
． MB=
（6分）．
由MF-MB<BD<MD+MB（8分）, (MF=MD)
得: 
（10分）
18． 解：用直尺测出木板的长为a，宽为b，知道a>b>0，又知道两墙面所成二面角为
（2分）．
设b作底边，a作直三棱柱的侧棱，底面另两边为x,y, 则
（4分）
（6分）
（8分）
则当x=y时，
（10分）同理，若a作底边，有
当x=y时，
∴
所以把长边放在底面，短边作侧棱，且围成底面是等腰三角形时，容积最大。（12分）
19． 解：设长方体的底面长，宽分别为x,y, 高为z．（2分）
则
由：（1）、（2），得
。（4分）
∵
∴
.（6分）
∵
.（8分）
将
的二次函数视为
的二次函数，它的增区间是[0，12].（10分）由于
，故当
，
取最大值128.
∴
的最大值为
.（12分）
20．（12分）证明：由题设，有
|
，
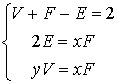
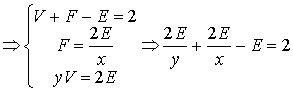由此得到所证等式.
21． (14分)．
（Ⅰ）证法一：∵点D是正△ABC中BC边的中点，∴AD⊥BC，
又A
证法二：连结A
∴A1D⊥BC ，∵BC∥B
（Ⅱ）解法一：作DE⊥AC于E， ∵平面ACC1⊥平面ABC，
∴DE⊥平面ACC1于E，即DE的长为点D到平面ACC1的 距离． 在Rt△ADC中，
AC=2CD=
∴所求的距离
（9分）
解法二：设点D到平面ACC1的距离为
，
∵体积
即点D到平面ACC1的距离为
．（9分）
（Ⅲ）答：直线A1B//平面ADC1，证明如下：
证法一：如图1，连结A
又DF
平面ADC1，A1B
平面ADC1，∴A1B∥平面ADC1． （14分）
证法二：如图2,取C1B1的中点D1，则AD∥A1D1，C1D∥D1B，
∴AD∥平面A1D1B，且C1D∥平面A1D1B，
∴平面ADC1∥平面A1D1B，∵A1B平面A1D1B，∴A1B∥平面ADC1． （14分）
22． 解：（1）因为SB在底面ABC上的射影AB与AD不垂直，否则与AB=AC且D为BC的中点矛盾，所以AD与SB不垂直；（4分）
（2）设
，则
解得 
，所以
（舍），
．
平面ABC，AB=AC，D为BC的中点
，
则
是二面角S—BC—A的平面角．
在
中，
,
故二面角的正切值为４；（9分）
（3）由（2）知，
平面SDA，所以平面SBC
平面SDA，过点A作AESD，则AE平面SBC，于是点A到平面SBC的距离为AE,
从而
即A到平面SBC的距离为
．（14分）