高二数学月考第二学期试卷
班级 姓名 学号 得分
一． 选择题（5×12）
1．a＞b，
，则（ ）．
（A）
（B）
（C）
（D）
2．不等式
的解集是（ ）
（A）（
（B）
（C）（0，1） （D）（0，1）
3．若
，x＞0，y＞0，则1gx＋1gy的最大值是（ ）．
（A）2 （B）2lg2 （C）－lg2 （D）lg2
4．不等式
的解集为
，则实数a的取值范围是（ ）．
（A）（3，
） （B）
（C）
（D）（
，－3）
5．直线m(x+y-1)+(3y-4x+5)=0不能化成截距式方程，则m的值为（ ）
(A) 5 (B) -3或4 (C) -3或4或5 (D) m∈（-∞，-3）∪（4，5）∪（5，+∞）
6．直线
：
x＋3y－1＝0 的倾斜角是
（ ）
（A）－
（B） （C）
（D）
７.下列说法正确的是 （ ）
（A）若直线l1与l2的斜率相等，则l1//l2（B）若直线l1//l2，则l1与l2的斜率相等
（C）若一条直线的斜率存在，另一条直线的斜率不存在，则它们一定相交
（D）若直线l1与l2的斜率都不存在，则l1//l
８．直线
关于直线
对称的直线方程为（ ）
（A）
（B）
（C）
（D）
９．已知两直线3x＋2y－3=0与6x＋my＋1=0互相平行，则它们之间的距离等于
(A) 4 (B) 
(C) 
(D)
10．到直线2x+y+1=0的距离等于
的点的集合是（ ）
(A) {（x，y）2x+y-2=0}
(B) {(x，y)2x+y=0}
(C) {(x，y)2x+y=0或2x+y-2=0}
(D) {(x，y)2x+y=0或2x+y+2=0}
11．直线
：3x+3y+8=0到直线
：
的角是（ ）
(A) 
(B)
(C) 
(D)
12．如图所示，直线l1：ax－y＋b＝0与l2：bx－y＋a＝0 (ab≠0,a≠b)的图象只可能是（ ）
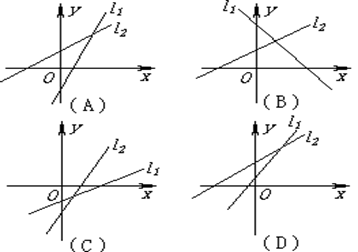
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（4×4）
13．设x、
，且
，则
的最小值是__________．
14．不等式
的解集是______________．
15．过点（10，-4）且倾斜角的余弦值是
的直线方程为
16．已知x, y满足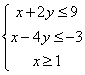
，则z=3x+y的最大值是
三、解答题
17、（12分）解下列不等式
（1）
（2）
18、（12分）过点P（2，1）作直线l交x轴、y轴的正半轴分别于A、B两点，当PA·PB取最小值时，求直线l的方程。
19.（12分）已知直线l1：x+my+6＝0,直线l2：(m－2)x+3y+
20．（12分）已知直线方程为(2+λ)x+(1-2λ)y+4-3λ=0
（1）求证不论λ取何实数值，此直线必过定点；
（2）过这定点引一直线，使它夹在两坐标轴间的线段被这点平分，求这条直线方程
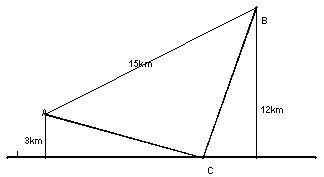21.（１2分） 已知Ａ、Ｂ两地距离为15ｋｍ，与公路Ｌ距离分别为３ｋｍ、１２ｋｍ，沃尔马公司计划在公路边Ｃ处建一大型超市，设计条件为Ｃ点到Ａ、Ｂ两地的距离之和最短（即
有最小值），请你根据学习过的解几知识，帮助沃尔马公司确定超市Ｃ的最佳位置。
22. （１4分） 制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损. 某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？