高中数学矩矩阵与变换综合测试
一、 选择题(每小题5分,共60分)
1、已知![]() ,且
,且 ![]() ,则n的值是( )
,则n的值是( )
A.3
B.-
2. ![]() =(3,-1),
=(3,-1), ![]() =(-1,2),则-3
=(-1,2),则-3![]() -2
-2![]() 的坐标是( )
的坐标是( )
A.(7,1) B.(-7,-1)
C.(-7,1) D.(7,-1)
3. 表示x轴的反射变换的矩阵是( )
A. 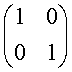 B.
B. 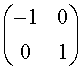 C.
C. 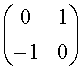 D.
D. 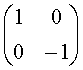
4.平面上任意一点在矩阵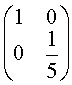 的作用下( )
的作用下( )
A. 横坐标不变,纵坐标伸长5倍
B. 横坐标不变,纵坐标缩短到![]() 倍
倍
C. 横坐标,纵坐标均伸长5倍 D. 横坐标,纵坐标均缩短到![]() 倍
倍
5.向量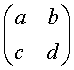 (左)乘向量
(左)乘向量![]() 的法则是( )
的法则是( )
A. 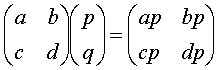 B.
B. 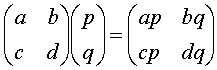
C. 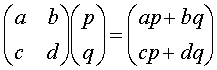 D.
D. 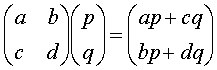
6. 变换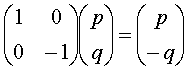 的几何意义为(
)
的几何意义为(
)
A.关于y轴反射变换 B. 关于x轴反射变换
C. 关于原点反射变换 D.以上都不对
7.点通过矩阵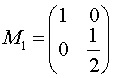 和
和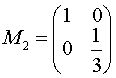 的变换效果相当于另一变换是( )
的变换效果相当于另一变换是( )
A. 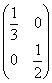 B.
B.
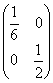 C.
C.
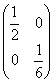 D.
D.
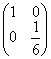
8.![]()
![]() 结果是( )
结果是( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
9.关于矩阵乘法下列说法中正确的是( )
A.不满足交换律,但满足消去律 B.不满足交换律和消去律
C.满足交换律不满足消去律 D.满足交换律和消去律
10.![]() ( )
( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
11.矩阵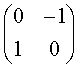 的逆矩阵是( )
的逆矩阵是( )
A. 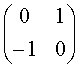 B.
B. 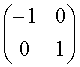 C.
C. 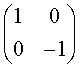 D.
D. 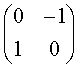
12.下列说法中错误的是( )
A.反射变换,伸压变换,切变都是初等变换 B.若M,N互为逆矩阵,则MN=I
C.任何矩阵都有逆矩阵 D.反射变换矩阵都是自己的逆矩阵
二,填空题(每小题5分,共20分)
13,给出下列命题:矩阵中的每一个数字都不能相等;二阶单位矩阵对应的行列式的值为1;矩阵的逆矩阵不能和原矩阵相等。其中正确的命题有 个。
14. 在矩阵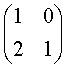 变换下,点A(2,1)将会转换成
。
变换下,点A(2,1)将会转换成
。
15,若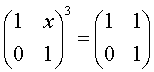 ,则
,则![]()
![]() 。
。
16,矩阵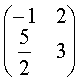 的特征值是
。
的特征值是
。
三解答题(共70分)
17,(体题10分)试讨论下列矩阵将所给图形变成了什么图形,并指出该变换是什么变换。
(1)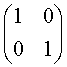 方程为
方程为![]() ;(3分)
;(3分)
(2)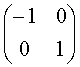 点A(2,5);(3分)
点A(2,5);(3分)
(3)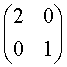 曲线方程为
曲线方程为![]() (4分)
(4分)
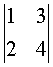
18. (本题12分)求下列行列式的值
(1)
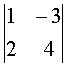
(2)
(3)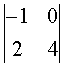
(4)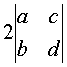
19,(本题5分)已知矩阵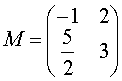 ,向量,
,向量,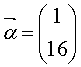 求
求![]()
20. (本题10分)已知ABC的坐标分别为A(1,1),B(3,2),C(2,4)
(1) 写出直线AB的向量方程及其坐标形式
(2) 求出AB边上的高
21,(本题10分)若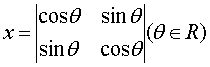 ,试求
,试求![]() 的最值。
的最值。
22. (本题13分)已知矩阵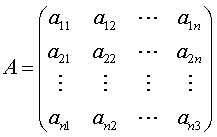 ,定义其转置矩阵如下:
,定义其转置矩阵如下: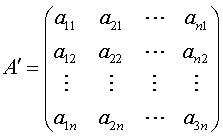
(1) 若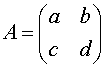 ,写出A的转置矩阵
,写出A的转置矩阵![]() ,并求行列式
,并求行列式![]() 和
和![]() ,两者有什么关系?
,两者有什么关系?
(2) 若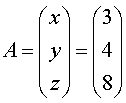 表示的方程组为
表示的方程组为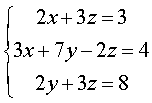 ,请写出
,请写出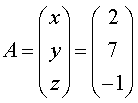 表示的方程组
表示的方程组
参考答案
1.C 2,B 3,D 4,B 5,C 6,B 7,D 8,A 9,B 10,A
11,A 12,C 13,1 14,(2,5) 15,〈 16,4或-2
17,(1)变换后的方程仍为直线,该变换是恒等变换
(2)经过变化后变为(-2,5),它们关于y轴对称,故该变换为关于y轴的反射变换
(3)所给方程是以原点为圆心,2为半径的圆,设A(x,y)为曲线上的任意一点,经过变换后的点我A1(x1,y1),则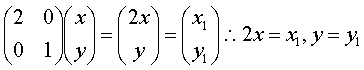
将之代入到![]() 可得方程
可得方程![]() ,此方程表示椭圆,所给方程表示的是圆,该变换是伸压变换。
,此方程表示椭圆,所给方程表示的是圆,该变换是伸压变换。
18,(1),-2 (2),10 (3),-4 (1),2(ad-bc)
19,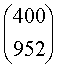
20,(1)AB的平行向量为:![]() ,设M为直线AB上任意一点,故所求向量方程为
,设M为直线AB上任意一点,故所求向量方程为![]() ,其坐标形式分别为
,其坐标形式分别为![]()
(2)![]()
21,当时,取得最小值-4
22,(1)由定义可知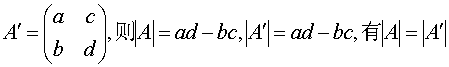
(2)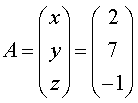 表示的方程组为
表示的方程组为