高二数学第二学期第一次月考试试卷
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），共150分，考试时间100分钟．
第Ⅰ卷（选择题共60分）
一、选择题（每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目
要求的．）
1．下列命题中，正确的个数是（ ）
①空间三点确定一个平面；
②经过空间三点有一个平面；
③经过圆上三点有且只有一个平面；
④两条直线确定一个平面。
A． 1个 B．2个 C．3个 D．1个或3个
2．已知命题“直线
上两点
在平面
内”，那么与此命题不等价的命题是（ ）
A．
B．平面过直线
C．直线上只有这两个点在内
D．直线上所有点都在内
3．一条直线和直线外不在同一条直线上的三点所确定的过该直线的平面有（ ）
A．1个 B．2个 C．3个 D．至多3个
4.空间不共线四个点
，在同一个平面内的射影
在同一直线上，那么可确定平面个数为（ ）
A．1 B．2 C．3 D．4
5．在空间，以下命题中真命题的个数为（ ）
①垂直同一条直线的两条直线平行；
②到定点距离等于定长的点的轨迹是圆；
③有三个角是直角的四边形是矩形；
④自一点向一条已知直线引垂线有且只有一条。
A．0个 B．1个 C．2个 D．3个
6．
，
与
都垂直，则的关系是（ ）
A．平行 B．相交
C．异面 D．平行、相交、异面都有可能
7．三个平面将空间分成的部分为
，则值为（ ）
A．4 B．4，6 C．4，6，7 D．4，6，7，8
8．设是异面直线，那么（ ）
A．必然存在唯一的一个平面同时平行于
B．必然存在唯一的一个平面同时垂直于
C．过直线
存在唯一的一个平面平行于直线
D．过直线存在唯一的一个平面垂直于直线
9．在空间，下列结论正确的是（ ）
A．过平面外一点，有且只有一个平面与已知平面平行
B．过一点，有且仅有一条直线与已知直线垂直
C．过平面外一点，有且仅有一条直线与已知平面平行
D．过直线外一点，有且仅有一个平面与已知直线平行
10．在正方体
中，
分别为
中点，则
是（ ）
A．正方形 B．菱形 C．矩形 D．空间四边形
11．直角三角形
的斜边
在平面内，顶点
在平面外，则
的两条直角边在平面内的射影与斜边组成的图形只能为（ ）
A．1条线段 B．1个锐角三角形
C．1个钝角三角形 D．1条线段或1个钝角三角形
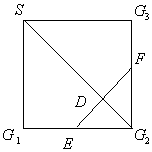12．如图，在正方形
中，
分别是
及
的中点，
是
的中点，现在沿
从把这个正方形折起，使点
重合，重合后的记为
，
那么下列结论成立的是（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题共90分）
二、填空题（每小题5分，共20分．）
13．三角形、四边形、正六边形、圆，其中一定是平面图形的有__________________.
14．若
，则
关系为___________________.
15．若
是所在平面外一点，
,
是线段
上一点，
是线段中点，则
=____________________．
16．如图，是直角三角形，
是斜边，三个顶点在平面的同侧，它们在内的射影分别为
，如果
是正三角形，且
，
，
，则的面积为___________________．
 |
三、解答题（共70分，其中第17、18、19小题13分、第20小题15分、第21小题16分．）
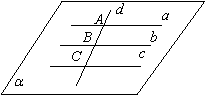
17．三条平行线都和第四条直线相交，求证这四条直线在同一平面内．
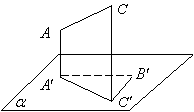
18．已知：四边形
中，
，
（或其延长线）分别与平面 相交于
四点．求证： 四点共线.
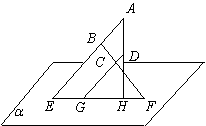
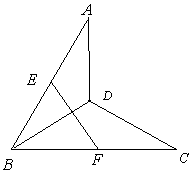
19．在空间四边形中，分别为
的中点．求证：和
为异面直线．
 |
20．正方体中，分别为
的中点．求
所成角的余
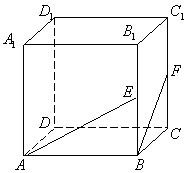弦值
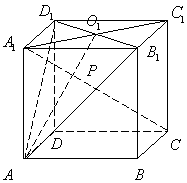21．正方体，
为上底面的中心，过顶点
作一个平面，此平面与对角线
交于点．求证：点必在线段
上．