高二数学第二学期期中考试

高二数学第二学期期中考试

班级＿＿＿＿姓名＿＿＿＿学号＿＿＿＿成绩＿＿＿＿

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合要求的，把答案填写在题中括号内.

1．下列事件 ：（1）．根据南通市气象台预报，明天晴；

　　　　　　　　　 （2）．海门中学所有高二在校 生中，至少有两名学生是同一 天生日；

　　　　　　　　　 （3）．由1，2，3，4，5五个数字组成五位数，这五位数能被3整除 ；

　　　　　　　　   （4）．sinθ+cosθ=,θ∈ R

中是随机事件的为（　　　　 ）

A．（1）、（2）　　　B．（1）、（3）　　　 C．（1）、（4）　　　　D．不同于A、B、C的结论

2．火星的半径约是地球的半径的一半，则地球表面积约是火星表面积的（　　　　 ）

A．倍　　　　　  B．2倍　　　　　　  C．4倍　　　　　　  D．8倍　

3．两个事件互斥是这两个事件对立的 （　　　　 ）

A．充分不必要条件　　　　　　　　　　　 B． 必要不充分条件　　　　　　 

C．充分 必要条件　　　　　　　　　　　　 D．既不充分也不必要条件

4．四个不同的球放入编号为1，2，3，4的四个盒子，则恰有一个空盒子的放法共有（　　　　  ）

A．228　　　　　　 B．144　　　　　　　　  C．96　　　　　 D．24

5．从5名男生4名女生中选4位 ，其中至少有2名男生，且至少有1名女生，分别参加数学、物理、化学、生物4门科目的竞赛辅导，不同的选择法有（　　　　 ）

A．100种　　　　　 B．400种　　　　　　 C．480种　　　　　　　 D．2400种

6． 展开式的常数项是 （　　　　  ）

A．－8　　　　　　  B．－12　　　　　　　  C．－20　　　　　　　 D．20

7．已知 ：100·101·102·103=，则n!·m的值为（　　　　  ）

A．100·101·102·103　　　　 B．99！　　　　　 C．2376　　　　 D．24

8．10人排成两列纵队，每列5人，共有（　　　　 ）

A．10！种 不同的排法　　　　　　　　　 B．种不同的排法　　　　　　　　

　  C．2×(5!)²种 不同的排法　　 　　　　D．2×种不同的排法

9．与的大小关系是（　　　　  ）

A．>　　　B．<　　　　 C．=　　　 D．大小关系随n的大小而定

10．在恒等式(1+x)ⁿ=a₀+a₁x+a₂x²+······+a_nxⁿ中，n∈N₊，且2a₄=3a_n－6，则 a₁+a₂+······+a_n的值为（　　　　  ）

A．2⁷　　　　　　　  B．2⁹　　　　　　　　　  C．2⁹ －1　　　　　  D．不同于A、B、C的结论

11．10件产品中有2件次品，现逐个进行检查，直至次品全部被查出为止，则第5次查出最后一个次品的概率为（　　　　　）

A．　　　　　　　  B． 　　　　　　　　C．　　　　　　  D．

12．设地球的半径为R，在北纬30⁰圈上有A、B两地 ，它们的经度差为120⁰，那么这两地间的纬线之长为（　　　　  ）

A．2πR　　　　　　 B．πR　　　　　　  C．πR　　　　 D．πR

二、填空题：本大题共4小题，每小题4分，共16分.把答案填写在题中横线上.

13．袋中有红、黄、绿3种颜色的球各1只，每次从中任取1只，有放回地抽取3次，则 3次颜色不全相同的概率为＿＿＿＿＿＿＿。

14．若 ，则 =＿＿＿＿＿＿＿。（答案可用一个组合数的形式表示即可）

15．将A，B，C，D四名同学按一定顺序排成一行，要求自左向右，

且A不排第一，B不排第二，C不排第三，D不排第四，请写出

他们四人所有不同的排法 ：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

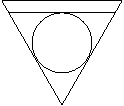
16．如图，有一轴截面为正三角形的圆锥形容器，内部盛水的高度为h，

放入一个球后，水面恰好与球相切，则球的半径为＿＿＿＿＿＿＿＿＿＿＿。

 

三、解答题：本大题共6小题，共74分.解答应写出必要的文字说明、证明过程及演算步骤 .

17．现有4名男同学，5名女同学，排成一横队。

（1）．男生、女士各在一边，有多少种不同的排法？

（2）．男女相间，有多少种不同的排法？

（3）．男生甲、乙排在一起，女生A排在女生B的右边，有多少种不同的排法？

18．抛掷两个均匀的正方体玩具（它的每个面上分别标以数1，2，3，4，5，6），它落地时向上的两数之和为几的概率最大？并写出这个概率。

19．A、B、C是半径为1的球面上的三点，B、C两点间的球面距离为，点A与B、C两点间的球面距离都为，球心为O，求 ：（1）．∠BOC，∠AOB的大小 ；（2）．球心O到截面ABC的距离。

20．已知 （n∈N₊）能被25整除，（1）．试求m的最小正值 ；

（2）．在（1）的结论下，求 (1+x)(1+2x)(1+3x)···(1+mx)的展开式中含x¹的项的系数 。

21．已知(3x－2y)ⁿ （n∈N₊）展开式的偶数项的二项式系数的和为1024，

（1）．求该展开式的二项式系数最大的项 ；

（2）．求该展开式的系数绝对值最大的项 ；

（3）．写出该展开式的系数最大的项，以及相应的项数 。

22．已知半径为R的球（球心为点O），在球内作一内接正四棱柱ABCD-A₁B₁C₁D₁，

（1）．求证 ：A、O、C₁三点共线 ；

（2）．设AB=x，AA₁=y，令点P的坐标为（x，y），求证 ：点 P的轨迹是某椭圆的一部分；

（3）．问当AB、AA₁分别为何值时，正四棱柱的侧面积最大 。　

一 ．选择题

1。D　　　　　  2。C　　　　　 3。B　　　　　  4。B　　　　　  5。D　　　　　　 6。C　　

7。C　　　　　  8。A　　　　　 9。D　　　　　  10。C　　　　  11。D　　　　　  12。D

二 。填空题

13。　　  14。　　15。BADC，BCDA，BDAC，CADB， CDAB，CDBA，DABC，DCAB，DCBA

16。

三 。解答题

17．（1）．　　　　 （2）．　　　 （3）．

18．　 7　　　　

19．（1）．∠BOC=　　∠AOB=　　  （2）．

20．（1）．m=6　　　　　 （2）．1+2+3+4+5+6=21

21. （1）．T₆=-　　 T₇=

（2）．T₅=　　（3）．T₅=

22.（1）．证明AC₁是大圆的直径

　　（2）．2x²+y²=4R²(x>0,y>0)

　　（3）．X=R,y=时，有S_max=4R²