高二数学期中试题参考答案
一、 选择题(本大题共12小题,每小题5分,共60分)
CBBCD ACAAB CD
二、 填空题(本大题共4小题,每小题4分,共16分)
13、![]() 14、
14、![]() 15、
15、![]() 16、
16、![]() (或
(或![]() )
)
三、 解答题(本大题共6小题,共74分.写出必要的解题步骤.)
17、解:设圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
则圆的方程为![]() .……………………………………2分
.……………………………………2分
由已知得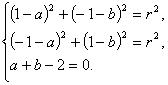 ………………………………………8分
………………………………………8分
解得![]() ………………………………………………………………10分
………………………………………………………………10分
所以圆![]() 的方程为
的方程为![]() .……………………………… 12分
.……………………………… 12分
18、解:由![]() 得交点
得交点![]() .……………………………………
4分
.……………………………………
4分
设直线![]() 的方程为
的方程为![]() 即
即![]() .……………… 6分
.……………… 6分
由点到直线的距离公式得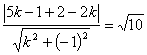 .
……………………8分
.
……………………8分
解得![]() .…………………………………………………………… 10分
.…………………………………………………………… 10分
所以直线![]() 的方程为
的方程为![]() .…………………………………… 12分
.…………………………………… 12分
19、解:由已知,双曲线的一条渐进线为![]() ,故可设双曲线的方程为
,故可设双曲线的方程为
![]() .……………………………
2分
.……………………………
2分
因为双曲线经过点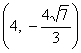 ,所以
,所以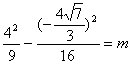 ,
,
解得![]() .
.
所以双曲线的方程为![]() .……………………………………
4分
.……………………………………
4分
所以![]() ,则
,则![]() ,且
,且![]() .
.
由双曲线的定义知,![]() ,(1)
,(1)
又在![]() 中,
中,![]() .(2)
.(2)
由(1)(2)联立,得![]() .………………………………… 8分
.………………………………… 8分
设点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,则
,则![]() ,………………10分
,………………10分
即![]() ,解得
,解得![]() .
.
即点P到x轴的距离为![]() .……………………………………………
12分
.……………………………………………
12分
或解:双曲线的方程求法如上…………………………………………… 4分
设![]() ,则由P
F1
,则由P
F1![]() P F2得
P F2得![]() ,
,
所以![]() ,即
,即![]() .(1)………………………
6分
.(1)………………………
6分
又点![]() 在双曲线上, 所以
在双曲线上, 所以 ![]() .(2)……………… 7分
.(2)……………… 7分
由(1)(2)得,![]() .……………………………………………10分
.……………………………………………10分
所以点P到x轴的距离为![]() .…………………………………………12分
.…………………………………………12分
20、解:设安排生产![]() 、
、![]() 种产品分别为
种产品分别为![]() 时,获得的利润为
时,获得的利润为![]() .
.
|
线性约束条件为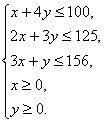 …… 4分
…… 4分
作出可行域,如图所示,…………………………………………… 6分
作直线![]() :
:![]() ,即
,即![]() ,
,
将直线![]() 平移至可行域内的点
平移至可行域内的点![]() 时,直线
时,直线![]() 在
在![]() 轴上
轴上
的截距最大,此时,![]() 最大.……………………………………………
8分
最大.……………………………………………
8分
由![]() 解得
解得![]() .
.
即当![]() 时,
时,![]() 最大.…………………………………………
10分
最大.…………………………………………
10分
答:安排生产![]() 、
、![]() 种产品分别为49件、9件时,能获得最大利润.12分
种产品分别为49件、9件时,能获得最大利润.12分
21、解:(1)由题意,设抛物线![]() 的方程为
的方程为![]() .
.
因为准线方程为![]() ,所以
,所以![]() ,即
,即![]() .
.
所以抛物线![]() 的方程为
的方程为![]() .………………………………………
3分
.………………………………………
3分
(2)由题意,设直线![]() 的方程为
的方程为![]() .
.
由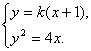 消去
消去![]() 得,
得,![]() .………
5分
.………
5分
则![]() .
(*).………………… 6分
.
(*).………………… 6分
设![]() ,由韦达定理得,
,由韦达定理得,
![]() .
.
所以![]() .
.
由中点坐标公式得,点![]() 的坐标为
的坐标为![]() ,
,
即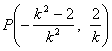 .……………………………………………………… 8分
.……………………………………………………… 8分
因为抛物线![]() 的焦点为
的焦点为![]() ,则由斜率公式得直线
,则由斜率公式得直线![]() 的斜率为
的斜率为
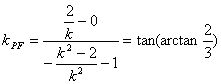 ,即
,即![]() ,
,
解得![]() ,或
,或![]() .……………………………………………………10分
.……………………………………………………10分
由(*)知![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .……………………12分
.……………………12分
22、解:(1)由题意,![]() ,即
,即![]() ,
,![]() .
.
又点![]() 在椭圆上,则
在椭圆上,则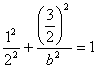 ,得
,得![]() ,
,
所以 ![]() .
.
则椭圆![]() 的方程为
的方程为![]() ,焦点为
,焦点为![]() ,
,![]() .…………4分
.…………4分
(2)设线段![]() 的中点
的中点![]() ,椭圆
,椭圆![]() 上的点
上的点![]() .
.
则由中点坐标公式得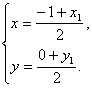 即
即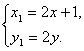
所以![]() ,即
,即![]() 为所求的轨迹方程.……8分
为所求的轨迹方程.……8分
(3)类似的性质:若![]() 是双曲线
是双曲线![]() :
:![]() 上关于原点对称的两个点,点
上关于原点对称的两个点,点![]() 是双曲线上任意一点,当直线
是双曲线上任意一点,当直线![]() 的斜率都存在,并记为
的斜率都存在,并记为![]() ,那么
,那么![]() 之积是与点
之积是与点![]() 位置无关的定值.10分
位置无关的定值.10分
下面证明:
设点![]() ,则
,则![]() ,其中
,其中![]() .
.
又设点![]() 为双曲线上任意一点,由
为双曲线上任意一点,由![]() ,
,![]() ,
,
得![]() .(*)
.(*)
将![]() ,
,![]() 代入(*)
代入(*)![]() .
.
即![]() 之积是与点
之积是与点![]() 位置无关的定值.………………………14分
位置无关的定值.………………………14分
