高二数学上学期期终测试卷
考试时间:120分钟 满分150分 可以使用计算器
| 得 分 | 评分人 |
一、填空题(本大题满分48分)本大题共有12题,只要求直接写出结果,每个空格填对得4分,否则一律得零分。
1.已知点A(3,13),B(-2,3),则直线AB的斜率是_________.
2.若Sn是数列{an}的前n项和,且![]() ,则
,则![]() =_______.
=_______.
3.若双曲线![]() 的两条渐近线互相垂直,那么,双曲线的左焦点坐标是___________.
的两条渐近线互相垂直,那么,双曲线的左焦点坐标是___________.
4.过点P(6,-2),且与直线y=-2x垂直的直线方程为__________。
5.若P是圆![]() 上的动点,则P到直线
上的动点,则P到直线![]() 的最小距离是_____。
的最小距离是_____。
6.公比为q的无穷递缩等比数列![]() 的所有项的和等于所有偶数项和的3倍,则q=
的所有项的和等于所有偶数项和的3倍,则q=
7.下面由火柴杆拼成的一系列图形中,第n个图形由n个正方形组成:

n=1 n=2 n=3 n=4
通过观察可以发现,第n个图形中,火柴杆共有___________根。
8.观察下列式子:![]() ,可以猜想一般的结论为:___________________________
,可以猜想一般的结论为:___________________________
9.已知F1、F2分别是椭圆![]() 的左右两个焦点,过F1作倾斜角为
的左右两个焦点,过F1作倾斜角为![]() 的直线与椭圆交于P、Q两点,则△F2PQ的面积为________.
的直线与椭圆交于P、Q两点,则△F2PQ的面积为________.
10.已知数列![]() 前n项和
前n项和![]() (b是常数),如果此数列是等比数列,则b=________.
(b是常数),如果此数列是等比数列,则b=________.
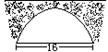 11.某桥洞呈抛物线形状,桥下水面宽
11.某桥洞呈抛物线形状,桥下水面宽
12.设F是椭圆![]() 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使FP1,FP2,FP3,…组成公差为d的等差数列,则d的取值范围为 .
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使FP1,FP2,FP3,…组成公差为d的等差数列,则d的取值范围为 .
| 得 分 | 评分人 |
二、选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选项、选错或者选出的代号代号一个(不论是否都写在括号内),一律得零分.
13.已知两条直线![]() ,当这两条直线的夹角在(
,当这两条直线的夹角在(![]() )内变动时,
)内变动时,![]() 的取值范围是( )
的取值范围是( )
A.(0,1) B.(![]() ) C.
) C.![]() D.(
D.(![]() )
)
14.过双曲线![]() 的右焦点,作直线
的右焦点,作直线![]() 交双曲线于A、B两点,若AB=2,则这样的直线存在( )
交双曲线于A、B两点,若AB=2,则这样的直线存在( )
A.1条 B.2条 C.3条 D.4条
15.以下各题中,方程为曲线的方程的是 ( )
(1)方程:x =3,曲线:经过点A(3,0)且垂直于x轴的直线。
(2)方程:x-y±![]() =0,曲线:与第一、三象限角平分线距离为1的点的轨迹。
=0,曲线:与第一、三象限角平分线距离为1的点的轨迹。
(3)方程:y -x=0,曲线:到x轴与到y轴的距离相等的点的集合。
(4)方程:x2+y2=4,曲线:与以原点为圆心,半径分别为1、3的两圆相切的圆的圆心轨迹。
(A)(1)、(2) (B)(2)、(3) (C)(2)、(4) (D)(1)、(4)
16.已知数列{![]() }的前n项和
}的前n项和![]() ,其中a、b是非零常数,则存在数列{
,其中a、b是非零常数,则存在数列{![]() }、{
}、{![]() }使得( )
}使得( )
A.![]() 为等差数列,{
为等差数列,{![]() }为等比数列 ;
}为等比数列 ;
B.![]() 和{
和{![]() }都为等差数列;
}都为等差数列;
C.![]() 为等差数列,{
为等差数列,{![]() }都为等比数列;
}都为等比数列;
D.![]() 和{
和{![]() }都为等比数列。
}都为等比数列。
三、解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.
17.(本题满分12分)在等差数列![]() 中,已知
中,已知![]() ,
,![]() 成公比为q的等比数列,求数列
成公比为q的等比数列,求数列![]() 的通项公式和公比q的值。
的通项公式和公比q的值。
18.(本题满分12分)已知直线2x+y+4=0与圆C:![]() 相切,圆C与x轴的负半轴交于A点,与y轴的正半轴交于B点,求
相切,圆C与x轴的负半轴交于A点,与y轴的正半轴交于B点,求![]() 的值。(结果用反三角函数值表示)
的值。(结果用反三角函数值表示)
19.(本题满分14分)
已知椭圆![]() (a>b>0)上的点
(a>b>0)上的点![]() 到两焦点的距离之和为
到两焦点的距离之和为![]() 。
。
(1)求椭圆的方程;
(2)过椭圆右焦点,倾斜角为![]() 的直线与椭圆相交于P,Q两点,求线段PQ的长。
的直线与椭圆相交于P,Q两点,求线段PQ的长。
20.(本题满分14分)已知点A(0,4),双曲线C:![]() 的渐近线经过点
的渐近线经过点![]() ,点P在双曲线的右支上。
,点P在双曲线的右支上。
(1)求AP的最小值及此时P点的坐标;
(2)设M,N是双曲线C上任意两点,线段MN的中点为B,若直线MN和直线OB的斜率存在,记为![]() ,求证:
,求证:![]() 是个常数。
是个常数。
21.(本题满分16分)某市2000年底有100万人,人均住房面积为10![]() ,由于政策移民等因素,人口年平均增长6%,为了改善市民的住房条件,市政府规定:从2001年起,每年新建住房60万
,由于政策移民等因素,人口年平均增长6%,为了改善市民的住房条件,市政府规定:从2001年起,每年新建住房60万![]() ,若2001年记作第一年。
,若2001年记作第一年。
(1)写出第n年该市的人口总数![]() (万人)和住房总面积
(万人)和住房总面积![]() (万
(万![]() );
);
(2)计算2006年底该市的人均住房面积,该数据说明什么问题?(精确到0.1![]() )
)
(3)按照这种新房建设速度,到2008年底,若要实现本届市政府提出的“人均住房面积达到![]() ”
”
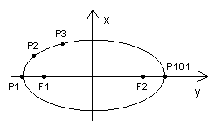
22.(本题满分18分)如图,已知![]() 均是椭圆
均是椭圆![]() 上的点,且P1,P101是长轴的两个端点,令
上的点,且P1,P101是长轴的两个端点,令![]() ,
,![]() 分别是数列{
分别是数列{![]() }和
}和![]() 的前n项和。
的前n项和。
(1)若{![]() }是等差数列,求数列{
}是等差数列,求数列{![]() }的公差d及{
}的公差d及{![]() }和
}和![]() 的通项公式;
的通项公式;
 (2对于(1)中数列{
(2对于(1)中数列{![]() },当2
},当2![]() 时,求n的取值范围;
时,求n的取值范围;
(3)若{![]() }是等比数列,令
}是等比数列,令![]() ,求数列
,求数列![]() 的最小值及此时n的取值。(精确到0.0001)
的最小值及此时n的取值。(精确到0.0001)
高二数学期终测试卷参考解答
一、填空题 1. 2 2. 3 3.
(-4,0) 4. x-2y-10=0 5.
5 6.
0.5 7. ![]()
8. ![]() 9.
9.
![]() 10.
-1 11. 2.6 12.
10.
-1 11. 2.6 12. ![]()
二、选择题 C A B C
三、解答题 17.解:由题意![]() …………4分
…………4分
解得![]() 或
或![]() …………8分
…………8分
所以an=15或者an=19-n…………10分
因而![]() 或q=1。…………12分
或q=1。…………12分
[注:缺少d=0,其它均正确,本题得8分]
18.解:由直线与圆相切求得![]() 或
或![]() …………2分
…………2分
当![]() 时,圆与x轴无交点。 …………4分
时,圆与x轴无交点。 …………4分
当![]() 时,圆的方程是
时,圆的方程是![]()
易求得C(1,-1),A(-1,0),B(0,1) …………7分
所以![]() ,
,![]() ,…………9分
,…………9分
![]() ,即
,即![]() 。…………12分
。…………12分
19.(1)由题意求得![]() 。…………5分
。…………5分
(2) 椭圆右焦点为(2,0),直线PQ方程为![]() …………7分
…………7分
由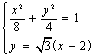 得
得![]() …………9分
…………9分
所以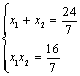 ,…………11分
,…………11分
![]() …………14分
…………14分
20.(1)双曲线C:![]() 的渐近线为
的渐近线为![]() ,将点
,将点![]() 的坐标代入求得
的坐标代入求得![]() ,双曲线方程为
,双曲线方程为![]() …………3分
…………3分
设P(x,y)(![]() ),则
),则![]() …………5分
…………5分
所以,当y=1时,AP的最小值为![]() ,此时P点的坐标为
,此时P点的坐标为![]() 。…………7分
。…………7分
(2)设![]() ,
,![]() ,
,![]() ,则
,则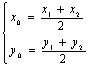
所以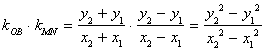 …………9分
…………9分
因为![]() ,
,![]() 在双曲线
在双曲线![]() 上,
上,
所以有![]() 和
和![]() …………11分
…………11分
两式相减得![]() 。…………14分
。…………14分
21.解:(1)由题意得![]() ,…………3分
,…………3分
![]() …………5分
…………5分
(2)由题意得![]() ,…………9分
,…………9分
这个数据说明:虽然政府加大了住房的建设速度,由于人口增长过快,老百姓的住房不但没有改善,反而不如以前. …………11分
(3)由题意得![]() ,…………14分
,…………14分
解得x![]() 0.7%
0.7%
所以,必须从2001起,将人口的增长率控制在![]() 0.7%以内,才能达到市政府提出的目标。…………16分
0.7%以内,才能达到市政府提出的目标。…………16分
22.解:(1)因为![]() ,
,![]() ,
,![]() …………2分
…………2分
所以,![]() ,
,![]() ,易求
,易求![]() ,…………4分
,…………4分
![]() ,
,![]() …………6分
…………6分
(2)![]() ,
,![]() …………8分
…………8分
由2![]() 得,
得,![]() ,解得
,解得![]() …………11分
…………11分
(3)由题意,![]() ,
,![]() ,…………13分
,…………13分
![]() …………15分
…………15分
令![]() 得n=74.2,因为
得n=74.2,因为![]() ,
,![]() ,……17分[只计算第74项扣1分]
,……17分[只计算第74项扣1分]
所以,当n=74时,![]() 的最小值为0.0545。…………18分
的最小值为0.0545。…………18分