高二数学试卷
第Ⅰ卷（选择题40分）
一、选择题： 本大题共10小题，每小题4分，共40分。在每题给出的四个选项中，只有一项是符合题目要求的。
1、下列函数中最小值是2的函数是( )
(A) 
(B)
(C) 
（D）
2、若直线
：ax+2y+6=0与直线
：x+(a-1)y+
-1=0平行或垂直，则a分别等于（ ）
(A) -1,2 (B) -1,
(C) 2,1 (D) ,-2
3、若关于x的不等式
的解集为φ，则a的取值范围是( )
（A）（3，+∞） （B）
3，+∞） （C）（-∞，3） （D）（-∞，3
4、当点(x ,y)在直线
上移动时 , 
的最小值是( )
（A）
（B）
（C）
（D）9
5、若
，则（ ）
（A）
（B）
（C）
（D）
6、已知点 A(2, -3), B( -3, -2) ,直线l过点(1 ,1)且与线段AB相交 ,则直线l的斜率的范围是( )
(A) 
≥
≤
(B) ≤≤
(C) ＜
(D)
≤≤4
7、若直线
始终平分圆
≤
的周长，则
的取值范围是（ ）
(A) 
(B) 
(C) 
（D）
8、已知实数
满足
≥
，则
的取值范围是（ ）
（A）
≤
或≥
（B）≤≤
（C）≤
或≥
（D）≤≤
9、过原点的直线与x2+y2+4x+3=0相切,若切点在第三象限，则该直线的方程为( )
(A)
(B) 
(C) 
(D) 
10、曲线
≤
≤
与直线
有两个交点时，实数的取值范围是( )
(A)
(B) 
(C) 
(D) 
第Ⅱ卷（非选择题，共60分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中的横线上 。
11、不等式(x－4)
≥0的解集是
。
12、已知
，且
则
的最大值是
。
13、直线
绕着点(1, 0)顺时针旋转90°，再将直线向上平移1个单位，这时恰好与圆
相切，则等于 。
14、已知圆
和直线
，当圆被直线截得的弦最短时，此时等于
。
三、解答题
15、（8分）已知为正实数，且
。①求
的最小值；②求
的最大值。
16、（8分）过点P(4,3)作直线l，直线l与的正半轴分别交于A，B两点，O为原点，当
最小时，求直线l的方程。
17、（8分）某家具厂有方木料90
，五合板600
，准备加工成书桌和书橱出售，已知生产每张书桌需要方木料0.1,五合板2，生产每个书橱需要方木料0.2,五合板1，出售一张书桌可获利润80元，出售一个书橱可获利润120元，怎样安排生产可得利润最大？
18、（10分）已知与曲线C：
相切的直线l交的正半轴与
两点，O为原点，
=
，
，
。（1）求线段
中点的轨迹方程；（2）求
的最小值。
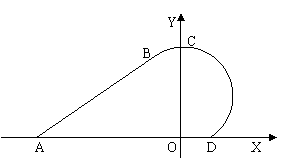
19、（10分）如图，圆弧
的圆心
在
轴上，直线切圆弧于
，若
，
，
（1）求曲线
的方程；（2）曲线和轴围成的图形面积。
 |