高二数学同步测试（10）—双曲线

高中学生学科素质训练

　

高二数学同步测试（10）—双曲线

一、选择题（本大题共10小题，每小题5分，共50分）

1．θ是第三象限角，方程x²+y ²sinθ=cosθ表示的曲线是　　　　　　　　　　　　　　　　　　　（ 　　）

　　　 A．焦点在x轴上的椭圆　　　　　　　　　　　　　B．焦点在y轴上的椭圆　　　　　　　　　　

　　　 C．焦点在x轴上的双曲线　　　　　　　　　　　 D．焦点在y轴上的双曲线

2．“ab<0”是“方程ax²+by ² =c表示双曲线”的　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．必要不充分条件　　　　　　　　　　　　　　　　 B．充分不必要条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．非充分非必要条件

3．一动圆与两圆：x²+y ²=1和x²+y ²-8x+12=0都外切，则动圆心的轨迹为　　　　　　　 （　　）

　　　 A．抛物线　　　　　　　　　　　　　　　　　　　　　　　 B．圆　　　　　　　　　　　　　　　　　　　　　　　　　　　C．双曲线的一支 　　　D．椭圆

4．双曲线虚半轴长为，焦距为6，则双曲线离心率是　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　　　D．

5．过点P（2，-2）且与-y ²=1有相同渐近线的双曲线方程是　　　　　　　　　　　　　　（ 　　）

　　　 A．　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　 D．

6．双曲线右支上一点P到右准线距离为18，则点P到右焦点距离为（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　　D．

7．过双曲线x²-=1的右焦点F作直线l交双曲线于A、B两点，若AB=4，这样的直线

有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1条　　　　　　　　　　B．2条　　　　　　　　　　C．3条　　　　　　　　　　　D．4条

8．双曲线3x²-y ²=3的渐近线方程是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．y =±3x　　　　　　　 B．y =±x　　　　　　 C．y =±x　　　　　　D．y =±x

9．双曲线虚轴的一个端点为M，两个焦点为F₁、F₂，∠F₁MF₂=120°，则双曲线的离心率为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　 D．

10．设双曲线（0<a<b）的半焦距为c，直线l过（a，0），（0，b）两点，已知原点到直线l的距离为c，则双曲线的离心率为　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．2　　　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　　　D．

二、填空题（本大题共4小题，每小题6分，共24分）

11．表示双曲线，则实数t的取值范围是　　　　　　　　　 ．

12．双曲线的准线方程是　　　　　　　　　　　　　　　  ．

13．焦点为F₁（-4，0）和F₂（4，0），离心率为2的双曲线的方程是　　　　　　　　  ．

14．设圆过双曲线的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离是　　　　　　　　　　　　　　　　 ．

三、解答题（本大题共6小题，共76分）

15．已知双曲线与椭圆共焦点，且以为渐近线，求双曲线方程．(12分)

16．双曲线的中心在原点，焦点在x轴上，两准线间距离为，并且与直线相交所得弦的中点的横坐标是，求这个双曲线方程．(12分)

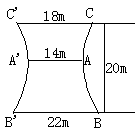
17．某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴（即双曲线的虚轴）旋转所成的曲面，其中A、A′是双曲线的顶点，C、C′是冷却塔上口直径的两个端点,B、B′是下底直径的两个端点，已知AA′=14m，CC′=18m，BB′=22m，塔高20m．建立坐标系并写出该双曲线方程．(12分)

18．F₁、F₂是的两个焦点，M是双曲线上一点，且，求三角形△F₁MF₂的面积．（12分）

19．一炮弹在A处的东偏北60°的某处爆炸，在A处测到爆炸信号的时间比在B处早4秒，已知A在B的正东方、相距6千米， P为爆炸地点，（该信号的传播速度为每秒1千米）求A、P两地的距离．(14分)

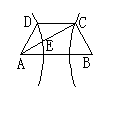
20．如图，已知梯形ABCD中AB=2CD，点E分有向线段所成的比为，双曲线过C、D、E三点，且以A、B为焦点．求双曲线的离心率．(14分)

参考答案

一．选择题（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	A	C	C	A	A	C	C	B	A

二．填空题（本大题共4小题，每小题6分，共24分）

11．t>4或t<1　　12．y= 　　　 13． 　 14．

三、解答题（本大题共6题，共76分）

15．(12分)　 [解析]：由椭圆．　

设双曲线方程为，则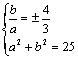　故所求双曲线方程为

16．(12分) [解析]：设双曲线方程为 （a>0，b>0），

　 ∵两准线间距离为，∴=，得c，　　①

　 ∵双曲线与直线相交，由方程组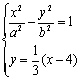　 得，

由题意可知，且　②

联立①②解得：，　所以双曲线方程为．

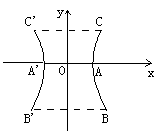17．(12分)　[解析]：（I）如图建立直角坐标系xOy，AA′在x轴上，AA′的中点为坐标原点O，CC′与BB′平行于x轴．　设双曲线方程为

则又设B（11，y₁），C（9，y₂），因为点B、C在双曲线上，

所以有　①

　 ②　　　　由题意知 ③　

由①、②、③得　故双曲线方程为

18．（12分）　[解析]：由题意可得双曲线的两个焦点是F₁（0，-5）、F₂（0，5），

　 由双曲线定义得：，联立得

　+=100=， 所以△F₁MF₂是直角三角形，从而其面积为S=

19．(14分)　[解析]：以直线AB为x轴，线段AB的垂直平分线为y轴，建立直角坐标系，

则A（3，0）、B（－3，0）　 　　

 右支上的一点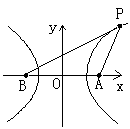　　　∵P在A的东偏北60°方向，∴．

　　　　 ∴线段AP所在的直线方程为

　　　　 解方程组　　 ，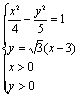

即P点的坐标为（8，）　　∴A、P两地的距离为=10（千米）．

20．(14分) [解析]：如图，以AB的垂直平分线为y轴，直线AB为x轴，建立直角坐标系，则CD⊥Oy．

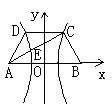由题意可设A（-c，0），C（，h），B（c，0），其中c为双曲线的半焦距，，h是梯形的高．　　　 由定比分点公式，得点E的坐标为

，．

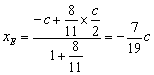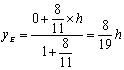设双曲线的方程为，由离心率．　 由点C、E在双曲线上，得

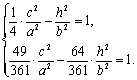　　由①得，代入②得　所以离心率