高二年级上学期数学期末复习

高二年级上学期数学期末复习

数　学　试　题

一、选择题：（本大题共１2题，每小题5分）

1．双曲线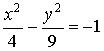的渐近线方程是　　　　　　　　　　  （　　　）

　　　　 A．　　　　 B．　　　　 C．　　　　 D．

2．程表示的曲线为 　　　　　　　　　　（　　　）

　　A. 抛物线　　　　　 B. 椭圆　　　　　　C. 双曲线　  　　　D.圆

3．物线y=4x²的准线方程为（　　）

A、x=－1　　　　 　B、y=－1　　　　　 C、x=　　　　  D、y=

4．线在点处的切线方程是（　　  ）

A、　　   B、 　　 C、　　　　 D、

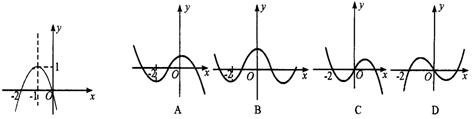5．已知函数f(x)的导函数的图像如左图所示，那么函数f(x)的图像最有可能的是右图中的　 （　　　）

 6．12、函数，已知在时取得极值，则=

A、2　　　　　　　　　　　　　　 B、3　　　　　　　　　　　　　 　C、4　　　　　　　　　　　 　 D、5

7．关于的方程有三个不同的实数解,则的取值范围 　　　　 （　 ）　 　　　　　　　　　　　　　　　 

A． (－∞，０)　　　　　　B．(－４，０)　　　　　　　　 C．(１，＋∞)　　　　　　　　　　 D．(０，１)

8．点在椭圆的左准线上，过点P且斜率为的光线经直线反射后经过椭圆的左焦点，则这个椭圆的离心率为　　　（　　　）

A．　　　 　　B．　　　　　　 C．　　 　　　　　 D．

9．双曲线的中心作直线与双曲线交于两点，则直线的倾斜角的范围是（　　  ）

A 　　 B 　　 C　　　 D

10．函数 在x=1处有极值-2，则a,　b的值分别为………………（　 　）

A．1，-3　　　　　 B．1，3　　　　　　 C．-1,3　　　　　　　　　 D．-1,-3　

11．圆内有一点，F为右焦点，椭圆上的点M使得│MP│+2│MF│的值最小，则点M为（　　）

 A．  　　　　B．　　　　C．　 　　　　D．　

12．已知为常数）在上有最大值，那么此函数在上的最小值为（  ）  A．　　　 B．　　　　 C．　　　　D．

二、填空题（本大共6小题，每小题5分，共30分）

13．过原点作曲线的切线，则切线的方程为　　　　　　　　　　　 ．

14．函数f(x)= cosx(sinx+1)+lnx,  则 =　　　　

15．设函数，集合，若，

则实数a的取值范围是_________

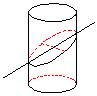
16．如图所示, 底面直径为的圆柱被与底面成的平面所截，

　　　 其截口是一个椭圆，则这个椭圆的长轴长　　　，短轴长　　 ，离心率为　　．

17．p：x+x－60,q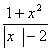：<0,则p是q的　　　　条件.

18．(1)已知，则_______.

(2)设函数。若是奇函数，则_______

三、解答题（本大题共6小题、共70分，解答给出文字说明，演算步骤）

19（10分）．求两条渐近线为且截直线所得弦长为的双曲线方程。

20（12分）．已知空间三点，，，设，

（1）求；（2）求实数，使与互相垂直．

21（12分）．如图，正三棱柱ABC-A₁B₁C₁中，AB=4，BB₁=6，　 D为AB的中点，　　　　　　　 F为A₁C₁中点，E在BB₁上，

 （1）当时，求异面直线CE与DF所成角的余弦　

（2）在侧棱BB₁上是否存在点P，使CP⊥DF，若存在，

求出BP的长；若不存在，请说明理由．

22（12分）．函数，已知是奇函数。

（Ⅰ）求、的值。

（Ⅱ）求的单调区间与极值。

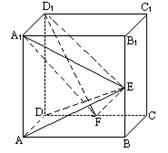23（12分）．如图,在正方体ABCD-A₁B₁C₁D₁中,E、F分别是BB₁、CD的中点.

(Ⅰ)证明AD⊥D₁F;(Ⅱ)求AE与D₁F所成的角;(Ⅲ)证明面AED⊥面A₁FD₁;

24（12分）．已知在与时，都取得极值．

(1) 求的值；(2)若，求的单调区间和极值；

(3)若对都有 恒成立，求的取值范围．