高二数学测试卷2

高二数学测试卷2

　　　　　　　  班级　　　 姓名　　　　

一．选择题：（本大题共12小题，每小题5分，共6 0分）

1．从6人中任选4人排成一排，其中甲、乙必须入选，且甲必须排在乙的左边（可 以不相邻），则所有不同排法的总数是…… (　 )

(A) 36　　　 (B) 72　 　　(C) 144　　  (D) 288

2．某篮球运动员在罚球线投中球的概率为，在某次比赛中罚3球恰好命中2球的概率为……（  ）

(A)　 　　(B)　　　　(C)　　　　 (D)

3.下列命题中正确的是（　 ）

（A）.垂直于同一直线的两条的直线平行;

（B）.若一条直线垂直于两条平行线中的一条，则它垂直于另一条；

（C）．若一条直线与两条平行线中的一条相交，则它与另一条相交；

（D）．一条直线至多与两条异面直线中的一条相交。

4．如图，在三棱柱的侧棱A₁A和B₁B上的点P，Q满足

A₁P=BQ，过P，Q，C三点的截面把棱柱分成两部分，

则这两部分的体积之比为……（　 ）

(A) 2∶1　 　 (B) 3∶1　　(C)4∶1  　　 (D)∶1

5．一个容量为20的样本数据分组后，组数与频数如下：，2；，3；，4；，5；，4；，2．则样本在上的频率为……( 　 )

(A)　　  (B)　　　　(C)　　　 (D)

6．在地球北纬60˚圈上有A、B两点，它们的经度相差180˚，则A、B两点沿纬度圈的弧长与A、B两点间的球面距离之比为……(　  )

(A) 1:3　　  (B) 3:1　　　(C)2:3　　　 (D) 3:2

7．若的展开式中含有常数项，则这样的正整数n的最小值是…… (　 )

(A)3　　　　(B)4  　　 (C)10　　　　(D)12

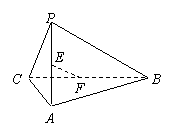
8．如右图，E、F分别是三棱锥P-ABC的棱AP、BC

的中点，PC=10，AB=6， EF=7 ,则异面直线AB与

PC所成的角为…… ( 　)

(A)60˚　　　 (B)45˚　　　 (C)30˚　　　(D)120˚

9．已知，，（其中为空间直角坐标系的三个正交基底）则与的数量积等于　　　　  （　　）

A、-15　　　　　　　　　 B、-5　　　　　　　　　　 C、-3　　　　　　　　　　 D、-1

10．从图中的12个点中任取3个点作为一组，

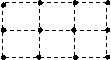其中可构成三角形的组数是……( 　)

(A)208　　 (B) 204　　 (C) 200　　　(D) 196

11．由等式定义，则等于……（ 　）

(A)　　(B)　　(C)　  (D)

12．已知集合A={12,14,16,18,20}，B={11,13,15,17,19}，在A中任取一个元素用a_i(i=1,2,3,4,5)表示，在B中任取一个元素用b_j(j=1,2,3,4,5)表示，则所抽取的数据满足a_i>b_j的概率为…… ( 　)

(A)　　  (B)　　　(C)　　  (D)

二．填空题：（本大题共4小题，每小题4分，共16分）

13．随机抽取甲、乙两位同学在平时数学测验中的五次成绩如下：

甲：69　77　75  68　86

乙：75　72　65  83　80

从以上数据分析，甲、乙两位同学数学成绩较稳定的是　　　　 同学．

14．若，，则．

15．在棱长为2的正方体 AC₁中，点E、F分别是棱AB、BC的中点，则点C₁到平面B₁EF的距离是　　　　．

16．给出下列四个命题：

① 若l∥a，则l平行于a内的每一条直线；

② 空间中，到定点的距离等于定长的点的轨迹是圆；

③ 曲线在点处的切线与直线x+y-3=0互相垂直；

④ 如果一个简单多面体的所有面都是四边形，那么F=V–2（其中F是面数，V是顶点数）．

其中正确命题的序号是：　　　　　　 ．

高二数学测试卷

一、选择题：（本大题共12小题，每小题5分，共6 0分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：（本大题共4小题，每小题4分，共16分）

 

13．　　　　　 　14．　　　　　 　 15．　　　　　  　16．　　　　　 

三、解答题：（本大题共6小题，共74分）

17．（本小题满分12分）

已知的展开式中第五项的二项式系数与第三项的二项式系数的比

是14∶3，求展开式中不含x的项．

18．（本小题满分12分）

如图，正三角形ABC与直角三角形BCD成直二面角，且ÐBCD=90°，ÐCBD=30°．

(1)求证：AB^CD；

(2)求二面角D-AB-C的大小；

(3)求异面直线AC和BD所成的角．

19．（本小题满分12分）

如右图，用A、B、C、D四类不同的元件连接成系统N，

当元件A正常工作且元件B、C都正常工作，或当元件A

正常工作且元件D正常工作时，系统N正常工作．已知

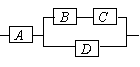A、B、C、D正常工作的概率依次为，，，．

(1) 求元件A、B、C都正常工作的概率；

(2) 求系统N正常工作的概率．

20．（本小题满分12分）

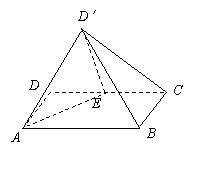已知E是矩形ABCD边CD的中点，且CD=2，BC=1．现沿AE将△DAE折起至△D′AE，使得D′到B、C两点的距离相等．

(1) 求证：平面D′AE⊥平面ABCE；

(2) 求二面角D′-BC-A的大小；

(3) 求点A到平面D′BC的距离．

21．（本小题满分12分）

甲、乙两人进行乒乓球比赛，采用“五局三胜制”，即五局中先胜三局者为胜．若每局比赛甲获胜的概率都是，乙获胜的概率都是．

求：(1)比赛以甲三胜一负而结束的概率；

(2)比赛以乙获胜而结束的概率．

22．（本小题满分14分）

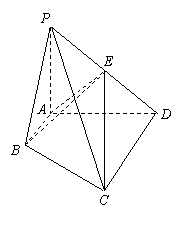如图，四棱锥P-ABCD的底面是直角梯形，ÐCDA=90°，AB∥CD，AB=CD，

PA^面ABCD，E为PD的中点．

(1) 证明：AE∥平面PBC；

(2) 当二面角P-CD-B为45°时，

证明：平面PBC^平面PCD；

(3) 在(2)的条件下，若AD=2，CD=4，

求三棱锥C-PBE的体积．