高中学生学科素质训练
高二数学测试题—排列组合（8）
一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．4名男歌手和2名女歌手联合举行一场音乐会，出场顺序要求两名女歌手之间恰有一名男歌手，共有出场方案（ ）种。 （ ）
A．
B．
C． D．A
A
A
2．编号为1，2，3，4，5，6的六个人分别去坐编号为1，2，3，4，5，6的六个座位，其中有且只有两个人的编号与座位编号一致的坐法有 （ ）
A．15种 B.90种 C．135种 D．150种
3．从6位男学生和3位女学生中选出4名代表，代表中必须有女学生，则不同的选法有（ ）
A．168 B．
4．氨基酸的排列顺序是决定蛋白质多样性的原因之一，某肽链由7种不同的氨基酸构成，若只改变其中3种氨基酸的位置，其他4种不变，则不同的改变方法共有 （ ）
A．210种 B．126种 C．70种 D．35种
5．某校刊设有9门文化课专栏,由甲,乙,丙三位同学每人负责3个专栏,其中数学专栏由甲负责,则不同的分工方法有 （ ）
A．1680种 B．560种 C．280种 D．140种
6．电话号码盘上有10个号码，采用八位号码制比采用七位号码制可多装机的门数是（ ）
A．
B．C
-C
C．
D．
7．已知集合A={1，2，3，4}，集合B={﹣1，﹣2}，设映射f: A→B，若集合B中的元素都是A中元素在f下的象，那么这样的映射f有 （ ）
A．16个 B．14个 C．12个 D．8个
8．从图中的12个点中任取3个点作为一组，其中可
构成三角形的组数是 （ ）
A．208 B．204
C．200 D．196
9．由0，1，2，3这四个数字可以组成没有重复数字且不能被5整除的四位数的个数是（ ）
A．24个 B．12个 C．6个 D．4个
10．假设200件产品中有3件次品，现在从中任取5件，其中至少有2件次品的抽法有（ ）
A．
种
B．(
)种
C．
种
D．
种
11．把10个相同的小球放入编号为1，2，3的三个不同盒子中，使盒子里的球的个数不小于它的编号数，则不同的放法种数是 （ ）
A．
B．
C．
D．
12.下面是高考第一批录取的一份志愿表。现有4所重点院校，每所院校有3 个专业是你较为满意的选择，如果表格填满且规定学校没有重复，同一学校的专业也没有重复的话，你将有（ ）种不同的填写方法. （ ）
A．
B．
C．
D．
| 志 愿 | 学 校 | 专 业 | |
| 第一志愿 | 1 | 第1专业 | 第2专业 |
| 第二志愿 | 2 | 第1专业 | 第2专业 |
| 第三志愿 | 3 | 第1专业 | 第2专业 |
二、填空题（本大题满分16分，每小题4分，各题只要求直接写出结果.）
13．由数字1、2、3、4、5组成没有重复数字，且数字1与2不相邻的五位数有_____个。
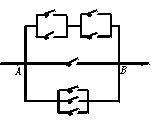14．一电路图如图所示，从A到B
共有 条不同的线路可通电.
15．在
的展开式中，含
项的系数是_________.
16．八名世界网球顶级选手在上海大师赛上分成两组,每组各四人,分别进行单循环赛,每组决出前两名,再由每组的第一名与另外一组的第二名进行淘汰赛,获胜者角逐冠亚军,败者角逐第三,第四名,则该大师赛共有____ 场比赛.
三、解答题（本大题满分74分.）
17．某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种，现在餐厅准备了 5种不同的荤菜，若要保证每位顾客有200种以上的不同选择，则餐厅至少还需准备不同的素菜品种多少种？
18．一些棋手进行单循环制的围棋比赛，即每个棋手均要与其它棋手各赛一场，现有两名棋手各比赛3场后退出了比赛，且这两名棋手之间未进行比赛，最后比赛共进行了72场，问一开始共有多少人参加比赛？
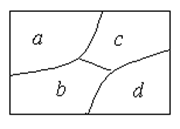
19．用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色，若相邻的区域不能用相同的颜色，则不同的染色方法的种数为 _______.
20．7名身高互不相等的学生，分别按下列要求排列，各有多少种不同的排法？
(1)7人站成一排，要求较高的3个学生站在一起；
(2)7人站成一排，要求最高的站在中间，并向左、右两边看，身高逐个递减。
(3)任取6名学生，排成二排三列，使每一列的前排学生比后排学生矮。
21．4位学生与2位教师并坐合影留念．(1)教师必须坐在中间；(2)教师不能坐在两端，但要坐在一起；(3)教师不能坐在两端，且不能相邻．各有多少种不同的坐法？
22．集合A与B各有12个元素,集合
有4个元素,集合C满足条件:
(1)
(2)C中含有3个元素; (3)
这样的集合C共有多少个?
高二下学期数学参考答案（8）
一、选择题
1D
5解：
8解：
9解：
二、本大题满分16分，每小题4分
13解：
72. 14解：
15解：2016；
16解：
三、解答题：本大题满分74分.
17解：设还需准备不同的素菜 x 种, x 是自然数，则
，即
，得
。
18解：设这两名棋手之外有n名棋手，他们之间互相赛了72-2×3=66场，
，解得：n=12.故一开始共有14人参加比赛。
19解：180
20解：（1）
（2）
（3）
=140。
21(1) 解法１ 固定法：从元素着眼，把受限制的元素先固定下来．
ⅰ) 教师先坐中间，有
种方法； ⅱ) 学生再坐其余位置，有
种方法． ∴ 共有 ·＝48种坐法．
解法２ 排斥法：从位置着眼，把受限制的元素予先排斥掉．
ⅰ) 学生坐中间以外的位置：；
ⅱ) 教师坐中间位置：．
解法３ 插空法：从元素着眼，让不受限制的元素先排好（无条件），再让受限制元素按题意插入到允许的位置上．
ⅰ) 学生并坐照相有种坐法； ⅱ) 教师插入中间：．
解法４ 淘汰法（间接解法）：先求无条件限制的排法总数，再求不满足限制条件的排法数，然后作差．即“A＝全体-非A”.
ⅰ) 6人并坐合影有
种坐法； ⅱ) 两位教师都不坐中间：
（先固定法）·；
ⅲ) 两位教师中仅一人坐中间； 
(甲坐中间) · 
(再固定乙不坐中间) · · 2（甲、乙互换）；
ⅳ) 作差：-（+2）
解法５ 等机率法：如果每一个元素被排入，被选入的机会是均等的，就可以利用等机率法来解．将教师看作1人（捆绑法），问题变成5人并坐照相，共有
种坐法，而每个人坐中间位置的机会是均等的，应占所有坐法的1/5，即教师1人坐
中间的坐法有
即
种。
(2) 将教师看作1人，问题变为5人并坐照相． 解法１ 从位置着眼，排斥元素——教师.
先从4位学生中选2人坐两端位置：；其他人再坐余下的3个位置：
；教师内部又有种坐法. ∴ 共有 ＝144种坐法．
解法2 从元素着眼,固定位置.
先将教师定位：
；再排学生： . ∴ 共有 种坐法。
(3) 解 插空法：（先排学生）
(教师插空).
22解：（1）若
，则这样的集合C共有
=56个；
（2）若
，则这样的集合C共有
个；
（3）若
且
，则这样的集合C共有
=160个。
综合（1），（2），（3）得：满足条件的集合C一共有56+4+160=220个。
