高二数学春季学期期中考试试卷
第Ⅰ卷
一、选择题
1、若点Q在直线b上，b在平面β内，则Q、b、β之间的关系可记作（ ）
A、Q∈b∈β B、Q∈b
β C、Qbβ
D、Qb∈β
2、“底面是正多边形，各侧棱与底面所成的角都相等”是棱锥为正棱锥的（ ）
A、充分但不必要条件 B、必要但不充分条件
C、充要条件 D、 既非充分又非必要条件
3、如图1，直三棱柱ABC-A1B
=
，则
=
，
=
，则
=（
）
A、+-
B、-+
C、-++
D、-+-
图1 图2
4、如图2，G、H、M、N分别是正三棱柱的顶点或所在棱的中点，则表示GH、MN是异面直线的图形有（ ）个：
A、0个 B、1个 C、2个 D、 3个
5、在空间，下列命题中正确的是（ ）
A、若两直线a、b与直线m所成的角相等，那么a∥b；
B、若两直线a、b与平面α所成的角相等，那么a∥b；
C、若直线m与两平面α、β所成的角都是直角，那么α∥β；
D、若平面γ与两平面α、β所成的二面角都是直二面角，那么α∥β。
6、如图3，Rt△ABC中，∠ACB=90°，直线m过点A
且垂直于平面ABC，动点P∈m，当点P逐渐远离A时，
∠PCB的大小（ ）
A、变大 B、变小
C、不变 D、有时变大，有时变小 图3
7、2000年10月，国际乒乓球赛的用球已由“小球”改为“大球”。“小球”的直径为
A、
B、19：
8、有玲、芳、玉、洁、静五位好朋友排成一排照相，其中玲、芳为一双同胞孪生姐妹，要求必须相邻，那么不同的排法共有（ ）种。
A、120
B、
9、已知二面角α-m-β为60°，A∈α，A到β的距离为1，则A在β内的射影A′到平面α的距离是（ ）
A、
B、
D、
10、将正方形ABCD沿对角线BD折成四面体ABCD，则直线AC与平面BCD所成的角不可能等于（ ）
A、90° B、60° C、45° D、 30°
11、设正多面体的每个面都是正n边形，以每个顶点为端点的棱有m条，棱数是E，面数是F，顶点数是V，则它们之间的关系不正确的是（ ）
A、nF=2E B、mV=2E C、V+F=E+2 D、 mF=2E
12、如图4代表未折叠正方形的展开图，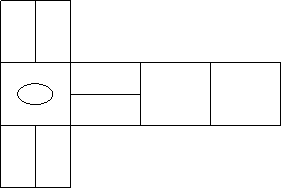
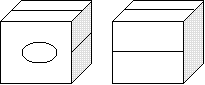将其折叠起来，变成正方体后，图形是（ ）
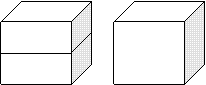A、
B、
图4
C、 D、
二、填空题：
13、已知=（2，-1，3），=（-4，2，x），且⊥，则x= 。
14、由数字0，1，2，3，4，5组成六位数，其中偶数共有 个。
15、一棱锥被平行于底的截面把其高分成长度相等的两部分，则棱锥的侧面被截成的两部分之比为 。
16、对于平面几何中的命题：“如果两个角的两边分别对应垂直，那么这两个角相等或互补。”在立体几何中，类比上述命题，可以得到命题：“
”，这个类比的命题真假性是 。
春季学期期中考试试卷
高二数学
第Ⅱ卷
一、选择题（12个小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(4个小题，每小题4分，共16分)
13、
14、 15、
16、
三、解答题（要求卷面整洁，应有解答过程。）
17、（12分）如图，BC=2，O是BC中点，点A坐标为（
，
，0），点D在平面yoz上，且∠BDC=90°，∠DCB=60°。
（1）求向量
坐标； （2）求向量
与
的夹角的大小。
18、（12分）如图：在底面是矩形的四棱锥P-ABCD中，PA⊥面ABCD，PA=AD，M、N分别是PC、AB的中点。
（1）求直线PD与面ABCD所成的角；
（2）试问：MN是异面直线AB、PC的公垂线吗？证明你的结论。
19、（12分）已知正三棱柱ABC-A′B′C′中，底面边长为6，过BC′作
平面BC′D∥AB′，AC交平面BC′D于D。
（1）求证：D为AC中点；
（2）求证：平面BC′D⊥平面ACC′A′。
20、（12分）如图，在直四棱柱ABCD-A1B
上变化时，求异面直线AC1与A1B1所成角的取值范围。
21、（12分）甲烷分子由一个碳原子和四个氢原子组成，其空间构型为一棱长为x的正四面体，碳原子位于该正四面体的中心，四个氢原子分别位于该正四面体的四个顶点上，若将碳原子和氢原子均视为一个点（体积忽略不计），且已知碳原子与每个氢原子间的距离均为a，求以四个氢原子为顶点的这个正四面体的体积。（结果用a表示）
22、（14分）如图，已知四棱柱ABCD-A1B
（1）求证：CC1⊥B1D1；
（2）当
的值是多少时，能使CC1⊥面B1CD1？请给出证明；
（3）当CC1⊥面B1CD1时，求二面角C1-B1D1-C的大小。