| 抽样测试高二数学试卷 |
|
一、选择题 (1)在等比数列{an}中,若a3、a9是方程3x2–11x+9=0的两个根,则a6等于( ) (A)3 (B)±3 (C)±Ö3 (D)-Ö3 (2)直线3x–4y+5=0关于x轴对称的直线方程为() (A)3x+4y–5=0 (B)3x+4y+5=0 (C)–3x+4y–5=0 (D)–3x+4y+5=0 (3)圆x2+y2=1上的点到直线3x+4y–25=0的距离的最小值是( ) (A)6 (B)4 (C)5 (D)1 (4)一个凸多边形的各内角的度数成等差数列,最小的是100°,最大的是140°,则这个多边形的边数是( ) (A)6 (B)8 (C)10 (D)12 (5)如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( ) (A)(0,+¥) (B)(0, 2) (C)(1, +¥) (D)(0, 1) (6)设x>0,y>0,A = x/(x+1),B = (x+y)/(x+y+1),则( ) (A)A>B (B)A=B (C)A<B (D)A、B的大小关系不能确定 (7) (A)0 (B)1/2 (C)2 (D)1 (8)不等式log1/2[Ö(x–3)–2] > 0的解集为() (A){xx<12} (B){x7<x<12} (C){xx>7} (D){xx>12} (9)已知直线l的倾角为q,满足p/6 < q < 2p/3,则l的斜率k的取值范围是() (A)(–Ö3/3, Ö3/3) (B)(–¥,–Ö3/3)∪( Ö3/3, +¥) (C)(–¥, –Ö3)∪( Ö3/3, +¥) (D)(–¥,–Ö3/3)∪( Ö3/, +¥) (10)椭圆x2/45+y2/20 = 1的两个焦点为F1、F2,P为椭圆上一点,若PF1^PF2,则PF1- PF2=( ) (A)2Ö5 (B)Ö5 (C)20 (D)4Ö5 二、填空题 (11)在等差数列{an}中,a1+a2=30,a3+a4=120,则a5+a6=________. (12)已知椭圆x2/25+y2/16=1上一点P到椭圆的一个焦点的距离为3,则点P到另一个焦点的距离为______. (13)过点M(2, 1)与原点的距离为2的直线方程为___________. (14)如果g (x) = f (x)+1 的最大值为1,则 f (x) 的最大值为____.
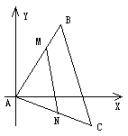
(15)已知a、b∈R+,且a+b=1,求证: (Ⅰ)ab≤1/4; (Ⅱ)1/a2+1/b2≥8. (16)解不等式 x > 1/(x–1). (17)已知A(0, 0),B(4, 8),C(6, – 4),点M在线段AB上,点N在 线段AC上,若AM:MB=3:1,△ABC的面积等于△AMN的2倍,求直线MN的方程. (18)甲,乙两人连续6年对某县农村养鸡业规模进行调查,调查后提供了两个不同的信息图: 甲调查表明:从第一年平均每个养鸡场生产1万只鸡上升到第六年平均每个养鸡场生产2万只鸡,如图甲;乙调查表明:由第一年养鸡场有30个减少到第六年有10个,如图乙.
请你根据提供的信息回答下列问题: (Ⅰ)第六年这个县的生产鸡数比第一年增加了还是减少了?说明理由. (Ⅱ)设第n年平均每个养鸡场生产只数为an,第n年的养鸡场个数为bn,写出an,bn的解析式(用n表示,1≤n≤6,n∈N) (Ⅲ)在这6年内,哪一年该县的生产鸡数的规模最大?说明理由. (19)在数列{an}中,已知a1 = 5,当n≥2 (n∈N)时,an = a1+a2+ · · · +an-1.
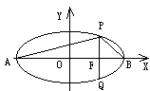
(Ⅱ)求证:1/a1+1/a2+ · · · +1/an < 3/5. (20)已知椭圆x2/a2+y2/b2=1的长轴两端点A、B,过焦点 F作弦PQ垂直于长轴AB.求证:不论a、b如何变化, 总有∠APB≠120°. 答案 一、 选择题 CBBAD CCBCA 二、 填空题(11)210; (12)7; (13)x=2或3x+4y–10=0; (14)2. 三、 解答题(15)略; (16){xx<1或x>(1+Ö5)/2}; (17)26x+3y–96=0; (18)(Ⅰ)减少;(Ⅱ)an=0.2n+0.8,bn=34– 4n;(Ⅲ)第2年; (19)(Ⅰ) |
 三、解答题
三、解答题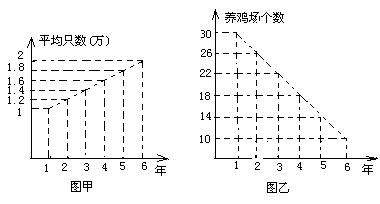
 (Ⅰ)求数列{an}的通项公式;
(Ⅰ)求数列{an}的通项公式;