第二学期3月份月考高二年级数学试卷
一、选择题：(本大题共12小题，每小题5分，共60分,在每小题给出的四个选项中，只有一项是符合题目要求的.)
1.已知等差数列
的通项公式为
, 则它的公差为( )
(A)2
(B)3
(C)
(D)
2.若
，则下列不等式中成立的是（ ）
(A)
(B)
(C)
(D)
3.
一个物体的运动方程为
其中
的单位是米，
的单位是秒，那么物体在
秒末的瞬时速度是（ ）
（A）
米/秒
（B）
米/秒 （C）
米/秒
（D）
米/秒
4.与椭圆
有相同焦点的双曲线方程是( )
(A)
(B)
(C) 
(D) 
5.双曲线
的渐近线方程为(
)
(A)
(B)
(C)
(D)
6.
已知
有极大值和极小值，则
的取值范围为(
)
（A）
（B）
（C）
或
（D）
或
7.下列有关命题的说法错误的是 ( )
(A)命题“同位角相等,两直线平行”的逆否命题为：“两直线不平行,同位角不相等”.
(B)
“
”是“
”的充分不必要条件.
(C)若
为假命题，则
、
均为假命题.
(D)对于命题
：
使得
, 则
：
均有
.
8.过点
与抛物线
只有一个公共点的直线有（ ）
(A)1条 (B)2条 (C)3条 (D)无数多条
9.设等比数列
的前n项和为
,且
, 则下列等式成立的是(
)
(A)
(B)
(C)
(D)
10.已知二次函数f(x)=a(x－m)(x－n)
，若不等式
的解集是
且不等式
的解集是
，则实数m、n、
、
的大小关系是( )
(A)
m＜＜＜n (B)＜m＜n＜
(C)m＜＜n＜ (D)＜m＜＜n
11．设函数
在区间
上是减函数，则
的取值范围（ ）（A）
（B）
（C）
（D）
12． 一同学在电脑中打出如下若干个圈：
○●○○●○○○●○○○○●○○○○○●…
若将此若干个圈依此规律继续下去,得到一系列的圈,则在前120个圈中的 ● 的个数( )
(A)12 (B) 13 (C)14 (D)15
二、填空题: 本大题共6小题,每小题5分,共30分,把答案填在答题卷中相应横线上.
13.双曲线
上一点
到它的一个焦点的距离等于1 , 那么点到另一个焦点的距离等于_______.
14.已知集合
,
,则
_________.
15. 函数
的导数为_________________．
16.约束条件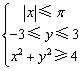
表示的平面区域的面积是
______平方单位.
17．函数
在区间
上的最大值是 ．
18．已知函数：（1）
（x<0），（2）
（
），（3）
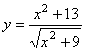，（4）
（），其中以4为最小值的函数的序号为______．（这里：
，
）
三、解答题：本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤 , 把答案写在答题卷上指定位置处 .
19．等差数列
不是常数列，
,且
是某等比数列
的第1，3，5项.
(1)求数列的第20项；
(2)求数列的通项公式.
20．已知函数
（为非零常数）.
（1）解不等式
；（2）若
恒成立，求的取值范围.
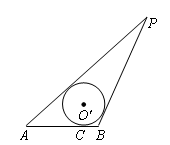21．如图，已知线段AB=4，动圆
与线段AB切于点C，且AC-BC=2
，过点A，B分别作⊙的切线，两切线相交于P，且P、均在AB的同侧.
⑴建立适当坐标系，当位置变化时，求动点P的轨迹E的方程；
⑵过点B作直线
交曲线E于点M、N，求△AMN的面积的最小值.
22．宽为a的走廊与另一走廊垂直相连，如果长为
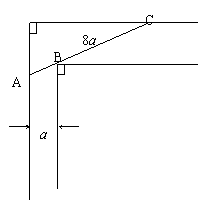通过拐角，向另一走廊的宽度至少是多少？
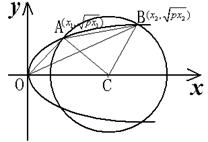
23. 如图，设圆
的圆心为C，此圆和抛物线
有四个交点，若在
轴上方的两个交点为
，坐标原点为O，
的面积为S.
⑴求的取值范围；
⑵求S关于的函数
的表达式及S的最大值；
⑶求当S取最大值时，向量
的夹角.