高二(下)期中数学测试卷

高中学生学科素质训练

　

高二下学期数学期中测试题

题号	一	二	三						总分
			17	18	19	20	21	22
得分

第I卷(选择题 共60分)

一.　  选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)

1. 已知　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．90°　　　　　　　　　 B．30°　　　　　　　　　 C．60°　　　　　　　　　 D．150°

2. 设M、O、A、B、C是空间的点，则使M、A、B、C一定共面的等式是　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．

C． 　　　　　　 D．

3. 正四棱锥的一个对角面与一个侧面的面积之比为，则侧面与底面的夹角为（　　）

　　A．　　　　　　　　　　 B．　　　　　　　　　　　C．　　　　　　　　　　　D．

4. 在斜棱柱的侧面中，矩形的个数最多是　　　　　　　　　　　　　　　　　  （　　）

　　　A．2　　　　　 　　 B． 3 　　　　　　　　C．4　　　　　  　 D．6

5. 四棱锥成为正棱锥的一个充分但不必要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．各侧面是正三角形　　　　　　 　　　 B．底面是正方形

　　　C．各侧面三角形的顶角为45度　　　　　 D．顶点到底面的射影在底面对角线的交点上

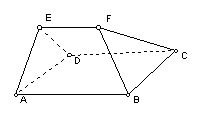6. 如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，，EF与面AC的距离为2，则该多面体的体积为　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　 B．5　　　　　　　　　　　　

　　　 C．6　　　　　　　　　　　　D．

7. 已知α，β是平面，m，n是直线.下列命题中不正确的是　　　　　　　　　　　　　　　　　 （　　）

　　　A．若m∥n，m⊥α，则n⊥α　　　　　　　 B．若m∥α，α∩β=n，则m∥n

　　　 C．若m⊥α，m⊥β，则α∥β　　　　　　 D．若m⊥α，，则α⊥β

8．已知点A（1，0，0），B（0，1，0），C（0，0，1），若存在点D，使得DB∥AC，DC∥AB，则D点的坐标是　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．（-1，1，1）　　　　　　　　　　　　　　　　　　　 B．

　　　 C．（-1，1，1）或（1，-1，-1）　　　　　　 D．

9. 下列命题中，正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 （1）各个侧面都是矩形的棱柱是长方体

　 （2）三棱锥的表面中最多有三个直角三角形

　 （3）简单多面体就是凸多面体

　 （4）过球面上二个不同的点只能作一个大圆

　 　Ａ.0个　　  　　　　 Ｂ.1个　　  　　　　 Ｃ.2个　　　　　　　Ｄ. 3个

10. 将鋭角B为60°, 边长为1的菱形ABCD沿对角线AC折成二面角,

若60°,120°, 则折后两条对角线之间的距离的最值为 　　　　（　　）

　　　 A. 最小值为, 最大值为　 　　　　　 B. 最小值为, 最大值为

　　　 C. 最小值为, 最大值为　 　　　　　 D. 最小值为, 最大值为

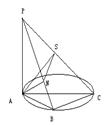11. 如图，AC为圆O的直径，B为圆周上不与点A、C

重合的点，PA垂直于圆O所在的平面，连结PB、

PC、AB、BC，作AN⊥PB，AS⊥PC，连结SN，

则图中直角三角形个数为　　　　　　　　　　　　　　（　　）

　　　 A．7　　　　　　　　　　　 B．8 　　　　　　　　　　　

　　　 C．9 　　　　　　　　　　　D． 10

12．设有如下三个命题：

　　 甲：相交的直线l，m都在平面α内，并且都不在平面β内；

　　 乙：直线l,m中至少有一条与平面β相交；

　　 丙：平面α与平面β相交 .

当甲成立时，　　　　　　　　　　　　　　　　　　　　　  　　　　　 （　　）

　　　 A．乙是丙的充分而不必要条件；　　　　　　B．乙是丙的必要而不充分条件

　　　 C．乙是丙的充分且必要条件　　　　　　　　D．乙既不是丙的充分条件又不是丙的必要条件.

第II卷（非选择题 共90分）

二、填空题（本大题共4小题，每小题4分，共16分）

13．边长为2的正方形ABCD在平面α内的射影是EFCD，如果AB与平面α的距离为，则AC与平面α所成角的大小是　　　　　　　　 　　　.

14.已知A（1，-1，3），B（0，2，0），C（-1，0，1）若点D在OZ轴上，且

　　　 则 　　　　　　　　　　　 .

15. 已知,,  ,若共同作用在物体上，使物体从点 (2,-3,2)移到（4，2，3），则合力所作的功　　 . 　

16.已知点P，直线，给出下列命题：

　　①若　　　　②若

③若　　　　　④若

⑤若

　　其中正确命题的序号是_______________.(把所有正确命题的序号都填上)

三、解答题（本大题共6题，共74分）

17.（本题满分10分）已知平面平面，直线，a垂直于与的交线AB，试判断a与 的位置关系，并证明结论.

18. （本题满分12分）已知正四棱柱ABCD—A₁B₁C₁D₁.AB=1，AA₁=2，点E为CC₁中点，点P为BD₁中点.

　 （I）证明EF为BD₁与CC₁的公垂线；

　 （II）求点D₁到面BDE的距离.

19．（本题满分12分）在正方体ABCD—A₁B₁C₁D₁中，O为正方形ABCD的中心，M为D₁D的中点.

（I）求证：异面直线B₁O与AM垂直；

（II）求二面角B₁—AM—C的大小；

（III）若正方体的棱长为a，求三棱锥B₁—AMC的体积．

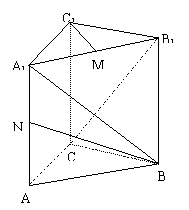20. （本题满分13分）如图，直三棱柱ABC-A₁B₁C₁，底面△ABC中，CA=CB=1，∠BCA=90º，棱AA₁=2，M、N分别是A₁B₁，A₁A的中点，

（I）求的长；

（II）求cos<,>的值；

（III）求证：A₁B⊥C₁M.

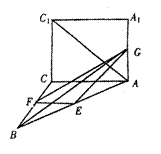
21. （本题满分13分）

如图，正方形ACC₁A₁与等腰直角△ACB互相垂直，∠ACB=90°，E、F分别是AB、BC的中点， G是AA₁上的点.

（I）若AC₁⊥EG，试确定点G的位置；

（II）在满足条件（1）的情况下，试求cos＜AC，GF＞的值.

22．（本题满分14分）如图，平面ABCD⊥平面ABEF，ABCD是正方形，ABEF是矩形，且G是EF的中点.

　 （Ⅰ）求证平面AGC⊥平面BGC；

　 （Ⅱ）求GB与平面AGC所成角的正弦值；

　 （Ⅲ）求二面角B—AC—G的大小.

高二(下)期中数学测试卷答案

一．选择题(本大题共12小题,每小题5分,共60分).

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	D	D	A	A	D	B	B	A	B	D	C

3解：设正四棱锥的底面边长为a,高为h,则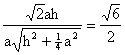，得记侧面与底面的夹角为选D.

6. 解：设AB,CD的中点分别为M,N, 则在多面体ABCDEF的体积等于三棱柱ADE-MNF的体积与四棱锥F-MNCB的体积之和，

　　　　　

，

多面体ABCDEF的体积等于选D．

12、提示：在甲成立时，乙成立，由平面三公理知，丙成立；反之也成立，选C．

二、填空题（本大题共4小题，每小题4分，共16分）

13．30º　  14. 　　 15. 　　　 16. ②⑤

三、解答题（本大题共6题，共74分）

17．解：a与的位置关系是：直线平面．

　 证明 过直线a作平面直线,（2分） ∵ ,∴.（4分）又∵∴.（6分）又∵，且，∴,（8分）故.（10分）

18．（1）证法一：取BD中点M.连结MC，FM .

　 ∵F为BD₁中点 ，　　∴FM∥D₁D且FM=D₁D .（2分）

　 又EC=CC₁且EC⊥MC ，∴四边形EFMC是矩形

　 ∴EF⊥CC₁.（4分） 又CM⊥面DBD₁ .∴EF⊥面DBD₁ .

　 ∵BD₁面DBD₁ . ∴EF⊥BD₁ .　故EF为BD₁ 与CC₁的公垂线.（6分）

　证法二：建立如图的坐标系，得

B（0，1，0），D₁（1，0，2），F（，，1），C₁（0，0，2），E（0，0，1）.（2分）

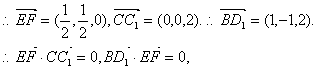
（4分）即EF⊥CC₁，EF⊥BD₁ .　

 故EF是为BD₁ 与CC₁的公垂线.（6分）

（Ⅱ）解：连结ED₁，有V_E－DBD1=V_D1－DBE .

由（Ⅰ）知EF⊥面DBD₁ ，设点D₁到面BDE的距离为d.

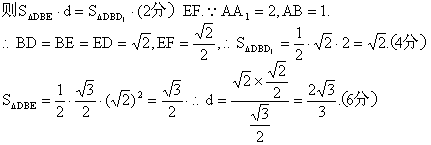
故点D₁到平面DBE的距离为.

19．9A中考查异面直线垂直的判定及二面角的求法；9B中考查利用向量证明线线垂直及利用数量积求二面角的大小的方法．

解法1（9A）：（1）设AD的中点为N，连结ON，由O为正方形ABCD的中心，

得ON⊥平面ADD₁A₁.又AA₁⊥平面ADD₁A₁，所以A₁N为B₁O在平面ADD₁A₁内的射影.（2分）在正方形ADD₁A₁中，

（2）因为AC⊥平面BB₁D₁D，所以AC⊥B₁O.由（1）知

B₁O⊥AM，所以B­₁O⊥AM，所以B₁O⊥平面AMC.　　　　 (6分)

作OG⊥AM于G，连结B₁G,则∠B₁GO为二面角B₁—AM—C的平面角.　　　 （7分）

设正方体棱长为1，则所以所以（9分）

（3）由（1）知，B₁O⊥平面AMC.所以V_B1－AMC=B₁O×S_△AMC

因棱长为a，所以B₁O=a，S_△AMC=×MO×AC=aa=a²

故V_B1－AMC=×a×a²=a³（12分）

解法2(9B)　 以D为原点，DA所在直线为x轴，DC所在直线为y轴，

DD₁所在直线为z轴，建立空间直角坐标系。

设正方体棱长为2，则M（0，0，1），O（1，1，0），

A（2，0，0），B₁（2，2，2）

（1）因OB₁=（1，1，2），AM=（－2，0，1），

AM ·OB₁=（1，1，2）·（－2，0，1）=1×（－2）+2×1=0，所以AM ⊥OB₁（4分）

（2）由（1）知AM ⊥OB₁，仿（1）可证CM ⊥OB₁，故OB₁ ⊥面AMC

又取BC中点为N（1，2，0），A₁（2，0，2），A₁N=（－1，2，－2），AB₁=（0，2，2）

A₁N·AB₁=（－1，2，－2）·（0，2，2）=0

A₁N·AM=（－1，2，－2）·（－2，0，1）=0，所以A₁N⊥面AB₁M，（7分）

于是二面角B₁—AM—C的平面角大小由A₁N与OB₁所成角确定，设其为θ，

cosθ===（9分）

（3）由上述可知，B₁O⊥平面AMC.所以V_B1－AMC=B₁O×S_△AMC

因棱长为a，所以B₁O=a，S_△AMC=×MO×AC=aa=a²

故V_B1－AMC=×a×a²=a³（12分）

20．解：（1）以射线、、分别为坐标系OX、OY、OZ轴，

则B（0，1，0），N（1，0，1），(2分)

==　　　　　(4分)

（2）A₁（1，0，2），B₁（0，1，2），C（0，0，0）

（1，-1，2），（0，1，2），　　　　 (6分)

∴cos<，>===.(8分)

　　（3）C₁（0，0，2），M（，，2），

=（，，0），（-1，1，-2）　　　 (10分)

∴·=×（-1）+×1+0×（-2）=0　

A₁B⊥C₁M.　　　　　　　　　　　　　　　　　 　(13分)

21． （满分13分）

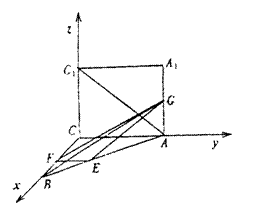解：（Ⅰ）由正方形ACC₁A₁与等腰直角△ACB互相

垂直，∠ACB=90°，∴BC⊥AC，∴BC⊥CC₁.以C

为坐标原点，建立空间直角坐标系C—xyz，

如图.（2分）

设AC=CB=a，AG=x，则A（0，a，0）.

C₁（0，0，a），G（0，a，x），E（-，，0）.

AC₁=（0，-a，a），EG=（-，，x）.（4分）

∵AC₁·EG=0，∴-+xa=0.

∴x=，∴G为AA₁的中点.（6分）

（Ⅱ）∵G（0，a，），F（，0，0），

∴GF=（，-a，-），AC₁=（0，-a，a）.（8分）

∴ GF =a， AC₁ =a，∴GF·AC₁=a²-=.

∴cos＜AC₁，GF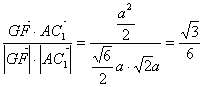＞=.（13分）

22．（Ⅰ）证明：正方形ABCD　 ∵面ABCD⊥面ABEF且交于AB，

∴CB⊥面ABEF　 ∵AG，GB面ABEF，　 ∴CB⊥AG，CB⊥BG

又AD=2a，AF= a，ABEF是矩形，G是EF的中点，

∴AG=BG=，AB=2a， AB²=AG²+BG²，∴AG⊥BG ∵CG∩BG=B ∴AG⊥平面CBG　而AG面AGC，　故平面AGC⊥平面BGC . (4分)

　 （Ⅱ）解：如图，由（Ⅰ）知面AGC⊥面BGC，且交于GC，在平面BGC内作BH⊥GC，垂足为H，则BH⊥平面AGC，　　∴∠BGH是GB与平面AGC所成的角

∴在Rt△CBG中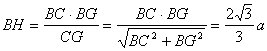　　又BG=，

∴.(9分)

　 （Ⅲ）由（Ⅱ）知，BH⊥面AGC　　　作BO⊥AC，垂足为O，连结HO，则HO⊥AC，

∴为二面角B—AC—G的平面角　 在

在Rt△BOH中，

即二面角B—AC—G的大小为.(14分)