高二第一学期期末数学考试

高二第一学期期末数学考试

　　　 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间为120分种。

第Ⅰ卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分；共60分。在每小题给出的四个选项中，只有

一项是符合题目要求的。

1．已知抛物线方程,则该抛物线的准线方程为　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　　　　B．　　　　　　 C．　　　　　　 D．

2．下列命题正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．若　　　　B． 若

　　　 C．若　　　　　　　　　　　D．

3．如果关于的方程为焦点在轴上的椭圆，则k的取值范围是（　　）

A．k>2　　　　　　　　　　B．1<k<2　　　　　　　　 C．1<k<3　　　　　　　　 D．2<k<3

4．已知方程表示的直线如图，则有　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．若C>0，则A>0，B>0

　　　 B．若C>0，则A<0，B>0

　　　 C．若C<0，则A>0，B>0

　　　 D．若C<0，则A>0，B<0

5．已知不等式的解集为（—∞，—1）∪（3，+∞），则对于函数，下列不等式成立的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　D．

6．过点（2，—2）且与有相同渐近线的双曲线方程是　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　 D．

7．已知满足的最小值为　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　 　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　D． 2

8．参数方程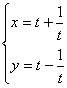　 表示曲线的离心率为　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　　　C．　　　　　　　　　　D．2

9．已知扇形面积为4，当该扇形周长最小时，半径为　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

10．直线与抛物线交于A、B两点，O为原点，则△AOB是　　　 （　　）

　　　 A．锐角三角形　　　　　　　　　　　　　　　　　　　　B．直角三角形

　　　 C．钝角三角形　　　　　　　　　　　　　　　　　　　　D．其形状不能确定

11．已知A（1，2）和B（3，—4）在直线的同侧，则k的取值范围是（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　　　 D．

12．已知函数，若。设　 ，则大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　 B． 　　　　　　　 C．　　　　　　　　D． 不确定

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题4分；共16分. 把答案填在题中横线上.

13．不等式的解集是　　　　　　  .

14．直线经过直线的交点，且与直线的夹角为45°，则直线的方程一般式为　　　　　　　 .,

15．已知△ABC，A（0，0），B（1，1）C（4，2），则△ABC外接圆的方程为　　　 .

16．已知下列四命题

①在直角作标系中，如果点P在曲线上，则P点坐标一定是这曲线方程的解；

②平面内与两个定点F₁ ­，F_2­­的距离的差的绝对值等于常数的点的轨迹叫做双曲线；

③角α一定是直线的倾斜角；

④直线关于轴对称的直线方程为

其中正确命题的序号是 　　　　　　　（注：把你认为正确命题的序号都填上）

三、解答题：本大题共6小题. 共74分.解答应写出文学说明、证明过程或演算步骤.

17．（本小题满分12分）

　　　 解不等式

18．（本小题满分12分）

　　　 已知圆，求在两轴上截距相等的该圆的切线方程。

19．（本小题满分12分）

　　　 某厂生产甲、乙两种产品，生产每吨甲、乙产品所需煤、电力和所获利润如下表所示：

消耗量　 资源 产品	煤（t）	电力（kW）	利润（万元）
甲产品	9	4	12
乙产品	4	5	6

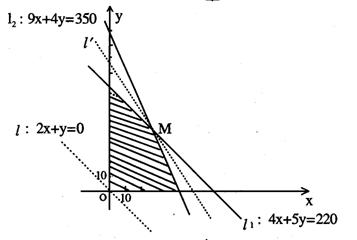
在生产这两种产品中，要求用煤量不超过350t，电力不超过220kW。问每天生产甲、乙两种产品各多少，能使利润总额达到最大？

20．（本小题满分12分）

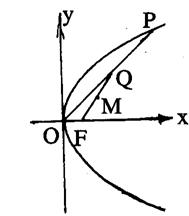
　　　 已知抛物线，焦点为F，顶点为O，点P在抛物线上移动，Q是OP的中点，M是FQ的中点，求点M的轨迹方程。

21．（本小题满分12分）

　　　 是否存在同时满足下列两个条件的椭圆：

　　　 （1）中心在作坐原点O，焦点F₁、F₂在轴上且长轴为4；

　　　 （2）PF₁、PO、PF₂成等比数列，其中P是椭圆上一点且PO=。

　　　 如果存在，求出该椭圆方程；如果不存在，说明理由。

22．（本小题满分14分）

设P、Q是函数（）图象上任意不同的两点，又

　　　 （Ⅰ）求的值；

　　　 （Ⅱ）求直线PQ的斜率的取值范围；

　　　 （Ⅲ）若，求函数图象上一点M到直线、直线距离之比的最大值。

高二数学试题参考答案及评分标准

一、选择题：CCDCA　 BACBB　 BA

二、填空题：

　　　 13． 　　　　　　　　　　　　　　　14．

　　　 15． 　　　　　　　　16． ①④

三、解答题：

　　　 17．解： 当时，原不等式可化为　　　　　　　　　　　　　　　　　　　　　 3分

　　　　　　　　　　　　 解得　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

　　　　　　　　　　　　 即

　　　　　　　　　　　　 则原不等式的解为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9分

　　　　　　　　　　　　 当时，原不等式可化为，该不等式恒成立　　　 11分

　　　　　　　　　　　　 所以，原不等式的解为　　　　　　　　　　　　　　　　　　　12分

　　　 18． 解：设所求圆的切线方程为　　　　　　　　　　　　　　　　　　　　　　　 2分

　　　　　　　　　　　　 ∵圆的标准方程为　

　　　　　　　　　　　　 ∴圆心为（0，1）半径r=1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

　　　　　　　　　　　　 由题意得：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

　　　　　　　　　　　　 解得：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

　　　　　　　　　　　　 所以，所求切线方程为　　　　12分

　　　 19． 解：设每天生产甲、乙两钟产品分别为t、t，利润总额为z万元。

　　　　　　　　　　 那么：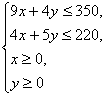　

　　　　　　　　　　　　 z=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 5分

　　　　　　　　　作出以上不等式组所表示的平面区域，即可行域

　　　　　　　　　作直线　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

　　　　　　　　　把直线向右上方平移至位置时，直线经过可行域上点M，现与原点距离最大

　　　　　　　　　此时z=取最大值。

　　　　　　　　　解方程组　 得M（30，20）　　　　　　　　　　　　　　　　　　　 11分

　　　　　　　　　答：生产甲产品30t，乙产品20t，能使利润总额达到最大。　　　　　　　　　12分

　　　 20． 解：设M（），P（），Q（）

　　　　　　　　　　　　 易求的焦点F的坐标为（1，0）

　　　　　　　　　　　　 ∵Q是OP的中点

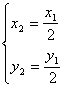　　　　　　　　　　　　 ∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

　　　　　　　　　　　　 又M是FQ的中点

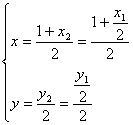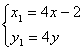　　　　　　　　　　　　 ∴　　即　　　　　　　　　　　　　　　　　8分

　　　　　　　　　　　　 ∵P在抛物线上

　　　　　　　　　　　　 ∴

　　　　　　　　　　　　 所以M点的轨迹方程为　　　　　　　　　　　　　　　　　　　　　　　 12分

21． 解：设满足（1）、（2）的椭圆方程为

　　　　　　　　　并设P（）、F­­₁（—c，0）、F­­₂（c，0）　　　　　　　　　　　　　　　　　　2分

　　　　　　　　　由题意PF₁·PF₂=PO­­_­­=3

　　　　　　　　　　　　　 PF₁+PF₂=2=4

　　　　　　　　　容易解出PF₁和PF₂的值是3和1或1和3，这里不妨设

　　　　　　　　　　　　　　PF₁=3，PF₂=1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

　　　　　　　　　即

　　　　　　　　　　

　　　　　　　　　将上述两方程相加并结合PO=　即

　　　　　　　　　解得：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

　　　　　　　　　所以

　　　　　　　　　这样满足题意的椭圆存在，其方程为　　　　　　　　　　　　 12分

22．解：（Ⅰ）由得：

　　　　　　　　　　　　 　　　 所以　　　　　　　　　　　　　　　　　　　　　　　 2分

　　　　　 （Ⅱ）由（Ⅰ）题设函数为

　　　　　　　　　　 设P、Q两点坐标分别为

　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

　　　　　　　　　　 ∵　　  ∴

　　　　　　　　　　 即直线PQ斜率的取值范围是（—3，1）　　　　　　　　　　　　　　　　　　　　　 8分

　　（Ⅲ）设点M坐标为（），M到直线的距离

　　　　，M到直线的距离

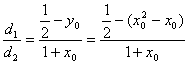　　　　则　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

　　　 令

　　　

　　　　　　　　　

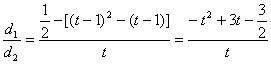
　　　　　　　　　当且仅当时，等号成立

　　　　　　　　　所以的最大值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分