重庆武隆中学2005～2006年高二数学期末模拟考试题
班级： 姓名： 考号： 成绩：
一、选择题（5*10=50分）
1、(x+1)(x+2)>0是(x+1)(
+2)>0的（ ）条件
A 必要不充分 B 充要 C 充分不必要 D 既不充分也不必要
2．若0<a<1，则下列不等式中正确的是 （ ）
A）(1-a)1/3>(1-a)1/2
B）log
(1+a)>0
C）(1-a)3>(1+a)2
D）(1-a)1+a>1
3.已知
，则
有
( )
A.最大值
B.最小值 C.最大值
D.最小值
4、已知
，则在不等式
表示的平面区域内的点是（ ）
A、
B、
C、
D、
5、已知坐标满足方程F（x，y）=0的点都在曲线C上，那么（ ）
A 曲线C上的点的坐标都适合方程F（x，y）=0；
B 凡坐标不适合F（x，y）=0的点都不在C上；
C 不在C上的点的坐标不必适合F（x，y）=0；
D 不在C上的点的坐标有些适合F（x，y）=0，有些不适合F（x，y）=0。
6、若抛物线
上一点P到准线和抛物线的对称轴的距离分别为
和
，则此点P的横坐标为（ ）
A 
B 
C
D
非上述答案
7、若焦点在
轴上的椭圆
的离心率为
，则m=（ ）
A 
B 
C 
D
8、已知
，则
的取值范围是（ ）
A 
B 
C 
D 
9、 已知椭圆
上一点P到它的右准线的距离为10, 则点P到它的左焦点的
距离是( )
A 8 B 10 C 12 D 14
10、与双曲线
有共同的渐近线,且经过点
的双曲线的一个焦点到
一条渐近线的距离是( )
A 1 B 2 C 4 D 8
二、填空题（4*6=24分）
11、设双曲线
的一条准线与两条渐近线交于A、B两点，相应的焦点为F，若以AB为直径的圆恰好过F点，则离心率为
12、抛物线
＝8上一点P到其焦点的距离为9，则其横坐标为___ ____。
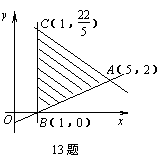13. 给出平面区域（如图），若使目标函数：z＝ax＋y（a＞０）取得最大值的最优解有无数多个，则a的值为
14. 不等式
的解集为
15. 椭圆
上到点A(1,0)的距离最近的点P的坐标是
16.已知x、y
，则使
恒成立的实数
的取值范围是
.
三、解答题（共74分）
17. 设a≠b. 解关于x的不等式. a2x+b2(1－x) ≥
18.若
，
，
是互不相等的正数，求证：
19、（12分）已知
+
=1的焦点F1、F2，在直线l：x+y－6=0上找一点M，
求以F1、F2为焦点，通过点M且长轴最短的椭圆方程．
]
20．(本小题满分14分) 要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格小钢板的块数如下表所示：
| 类 型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
|
,第二种为
,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小？
21、（12分）给定双曲线
。过A（2，1）的直线与双曲线交于两点
及
，求线段的中点P的轨迹方程．
22．（本小题满分14分）
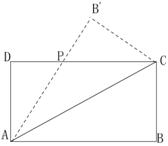
如图，设矩形ABCD（AB>BC）的周长为24，把它沿AC折起来，AB折过去后交DC于点P，设AB=x，求△ADP的面积S的表达式，以及 S的最大值及相应的x的值。
武隆中学2005～2006年高二数学期末模拟考试题（答案）
一、选择题
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | A | B | C | C | D | B | A | C | B |
二、填空题（4×4=16分）
11、
12、7 13. 14.
15. (
) 16. [2，+
三、解答题（共74分）
17.解: a2x+b2(1－x) ≥a2x2+b2(1－x)2+2abx(1－x)
a2x(1－x)+ b2(1－x)x－2abx(1－x) ≥0
x(1－x)(a－b)2 ≥0
∵a ≠b. (a－b)2>0
∴x(1－x) ≥0
∴0≤x≤1
18．
证: ∵a
+b≥2a
b,b+c≥2bc,c+a≥2ac
又 ，，是互不相等的正数 ,以上三式相加
∴a+b+c>ab+bc+ca,
同理可得:ab+bc+ca>ab•bc+bc•ca+ca•ab=abc(a+b+c)
19、（12分）已知+=1的焦点F1、F2，在直线l：x+y－6=0上找一点M，
求以F1、F2为焦点，通过点M且长轴最短的椭圆方程．
解：由
，得F1（2，0），F2（-2，0），F1关于直线l的对称点F1/（6，4），连F1/F2交l于一点，即为所求的点M，∴2a=MF1+MF2=F1/F2=4
，∴a=2，又c=2，∴b2=16，故所求椭圆方程为
．
20．解：设需截第一种钢板
张,第二种钢板
张,所用钢板面积为
,
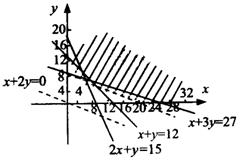则有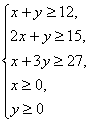
作出可行域(如图)
目标函数为
作出一组平行直线
(t为参数).由
得
由于点
不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使
最小,且
.
答:应截第一种钢板4张,第二种钢板8张,或第一种钢板6张,第二种钢板7张,得所需三种规格的钢板,且使所用的钢板的面积最小.
21、（12分）给定双曲线。过A（2，1）的直线与双曲线交于两点及，求线段的中点P的轨迹方程．
解：设
，
代入方程得
，
．
两式相减得： 
。
又设中点P（x,y），将
，
代入，当
时得
。又
， 代入得
。
当弦
斜率不存在时，其中点P（2，0）的坐标也满足上述方程。因此所求轨迹方程
是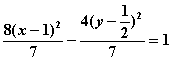
。
22.解：由P向AC作垂线交AC于E点（图略），则△PCE与△CAB相似，所以有：
，
又CE=
AC，
，
设AB=x，BC=12-x，由AB>BC，可得: 6<x<12，
，
从而 PC=
，DP=
，
△ADP的面积S=
，
所以S
，
当S取最大值时，x满足
，所以x=
。