不等式的证明练习
1．已知
，求证：
．
2．设a、
R，求证：
．
3．设
R，求证：
．
4．设
N*，求证：
．
5．设a、b、c、分别是△ABC中∠A、∠B、∠C的对边，求证：
．
6．若
，求证：
．
7．若0＜x＜1，求证：
．
8．设
，求证：
．
9．已知：
，
，
．
求证：
，
，
．
参考答案
1．
．
2．
．
3．用判别式法证明．
4．由
及
，再由不等式的同向可加性即得．
5．
．
6．换元
即可得证．
7．
．
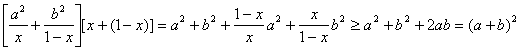8．
．
9．用反证法，假设结论不成立，由xyz＞0知x、y、z中应有两个负数，一个正数，不妨设x＞0，y＜0，z＜0．由已知条件，得：
x＞－（y＋x）＞0，
yz＞－x（y＋z）＞0，
，
即
，
亦即
，矛盾．