第六章 不等式
第一单元 不等式的性质
[知识要点]
1、不等式的性质
| 性质 | 内容 |
| 对称性 | a>bÛb<a；a<bÛb>a. |
| 传递性 |
|
| 加法性质 |
|
| 乘法性质 |
|
| 指数运算性质 |
|
| 倒数性质 |
|
.
； 
.
； 
； 
.
； 
.2、含绝对值不等式的性质
| 加法性质 | a-b£a±b£a+b； a1+a2+…+aN£a1+a2+…+aN. |
| 乘法性质 | ab=ab |
| 除法性质 |
|
（b¹0）.[典型例题]
例1、巳知a>b>0，c<d<0，e<0，求证
.
例2、设a和b都是非零实数，求不等式a>b和
同时成立的条件.
例3、若a>0，bc>a2，且满足a2-2ab+c2=0，判断a、b、c的大小.
例4、巳知正实数a、b、c满足
a+d=b+c，且a-d<b-c，求证ad>bc
例5、求证不等式
x+x1+x2+x3+…+xn³x-（x1+x2+…+xn）.
例6、设a、b为实数，且a¹b，
，求证a+b<f（a）+f（b）.
例7、设f（x）=x2+px+q，求证f(1),f(2),f(3)中至少有一个不小于
.
例8、设f（x）=ax2+bx+c，系数a、b、c都是实数，a¹0，b£a，f(-1)£1，
f(0)£ 1，f(1)£ 1，求证当x£1时，f（x)£
.
[测试题]
一、选择题
1、巳知命题“a³bÞc³d”和“a<bÞe£f”，则下列命题中正确的是（ ）
（A）e³fÞc³d （B）c£dÞe<d （C）e<fÞc<d （D）c<dÞe£f
2、巳知P=a+b-c，Q=b+c-a，T=c+a-b，其中a、b、c均为正数，则P>0，Q>0，T>0同时成立是PQT>0成立的（ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既非充分也非必要条件
3、巳知x<a<0，则下列各不等式中一定成立的是（ ）
（A）x2<ax<a2 （B）x2< a2< ax （C）x2> ax> a2 （D）x2> a2> ax
4、若x<5，nÎN*，下列5个不等式：
①
②
③
④
⑤
中，一定成立的有（ ）
（A）0个 （B）1个 （C）2个 （D）3个以上
5、巳知a、b、x是任意 实数，则下列不等式中一定成立的是（ ）
（A）x-a+b-x+x+a+b³3x （B）x-a+b-x+x+a+b£3x
（C）x-a+b-x+x+a+b>3x （D）x-a+b-x+x+a+b£3x
二、填空题
6、巳知实数a、b、c、d满足下列三个条件：①d>c；②a+b=c+d；③a+d<b+c.
把a、b、c、d按从大到小的顺序重新排列，并用>号连接起来是 .
7、设a>b>c>0，
，
则在l12，l22，l32，l1l2，l1l3和l2l3中最小的一个是 .
8、巳知x>y>z，且x+y+z=0，现有下列四个不等式：①xy>yz；②xz<yz；③xy>xz；
④xy>zy。请将正确的不等式的序号写出来： .
9、不等式
成立的充分必要条件是
.
10、若实数a、b满足a>b，则在不等式
，(a+1)2>(b+1)2,(a-1)2>(b-1)2中不正
确的有 个.
三、解答题
11、求证a>0是a>b且成立的必要不充分条件.
12、求证对实数a、b、m和n，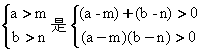
成立的充分必要条件.
13、设-1<a<1，证明
.
14、对实数a、b、c，证明：
a+b+c-a+b-b+c-c+a+a+b+c³0.
15、巳知a、b、c是实数，函数f(x)=ax2+bx+c，g(x)=ax+b，
且当-1£x£1时，f(x) £1。
（1） 证明c£1.
（2） 证明当-1£x£1时，g(x)£2.
（3） 设a>0，当-1£x£1时，g(x)的最大值为2，求f(x).