云南弥勒一中高二数学2005-2006学年第一学期
期末考试题中学试卷网版权所有 http://www.shijuan.cn
测试范围：高二（上）的全部内容
注意事项：本试卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷选择题，请用2B铅笔填涂在机读卡上；第Ⅱ卷为非选择题，请用黑色笔答在答题卡上。（考试时间：120分钟；考试形式：闭卷）
第Ⅰ卷 (选择题，共60分)
一、中学试卷网版权所有 http://www.shijuan.cn选择题（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，有一项是符合题目要求的.）
1、设
，现给出下列5个条件：①
;②
;③
;④
;⑤
,其中能推出“
,
中至少有一个大于1”的条件为（ ）
(A)②③④ (B)②③④⑤ (C)①②③⑤ (D)②⑤
2、若直线
经过第一、二、三象限，则（ ）
(A)
(B)
(C)
(D)
3、若不等式组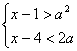
的解集非空，则实数的取值范围是（ ）
(A) （-1，3） (B)（-3，1） (C)（-∞，-1） (D)（-∞，-3）∪（1，+∞）
4、“>1”是直线
与直线
有且仅有两个交点的（ ）
(A)充分不必要条件 (B)必要不充分条件 (C)充分必要条件 (D)既不充分也不必要条件
5、
是过抛物线
的焦点弦，且
，则的中点到直线
的距离是（ ）
(A)
(B)2
(C)
(D)3
6、用一个与圆柱母线成
角的平面截圆柱，截口是一个椭圆，则此椭圆的离心率是（ ）
(A)
(B)
(C)
(D)
7、已知
， 则
有（ ）
(A)最大值
(B)最小值 (C)最大值1
(D)最小值1
8、已知直线
与圆
相切，则直线
的一个方向向量
为 ( )
(A)（2，-2） (B)（1，1） (C)（-3，2） (D)（1，）
9、已知函数
在
上
恒成立，则的取值范围是（
）
(A)
(B)
(C)
(D)
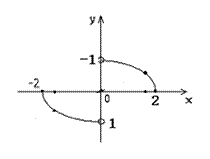
10、如图,函数
的图象是中心在原点,焦点在
轴上的椭圆的两段弧,则不等式
的解集为 （ ）
（A）
（B）
（C）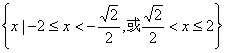
（D）
11、已知动点
满足
，则此动点
的轨迹是（ ）
(A)椭圆 (B)双曲线 (C)抛物线 (D)两相交直线
12、已知椭圆的一个焦点和对应的准线分别是抛物线
的焦点与准线，则椭圆短轴的右端点的轨迹方程是（ ）
(A)
(B)
(C)
(D)
第Ⅱ卷(非选择题 共90分)
二、填空题（本大题共4小题；每小题4分，共16分.把答案填在题中的横线上.）
13、若直线
始终平分圆
的圆周，则
的最小值为
14、是椭圆
上的动点，则
的的取值范围是
15、已知一椭圆的两焦点为
，有一斜率为
的直线被椭圆所截得的弦的中点为（2，1），则此椭圆方程为
16、给出下列四个命题
①两条直线平行的充要条件是它们的斜率相等；②过点
与圆
相切的直线方程为
；③平面内到两定点的距离之和等于常数的点的轨迹是椭圆；④抛物线上任意一点
到焦点的距离等于该点到准线的距离。
其中正确命题的序号是 （把你认为正确的命题序号都填上）
三、解答题(本大题共6小题；共74分.解答过程应写出文字说明、证明过程或演算步骤.)
17、（本小题满分12分）
已知
，且
成等比数列，求证：
18、（本小题满分12分）
已知
，求不等式
的解集。
19、（本小题满分12分）
已知圆
与圆
：
外切，且两圆的公切线为
，已知圆的圆心落在直线
上，求圆的方程。
20、（本小题满分12分）
设直线
与圆
交于
两点，且关于直线
对称，求不等式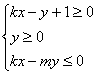
表示的平面区域的面积。
21、（本小题满分12分）
已知正三角形ABC的两顶点A,B在轴上，另一顶点在
轴上，DE为平行于轴的正ABC的中位线，双曲线M经过D,E两点，且以A,B为焦点，试求此双曲线的离心率
的值。
22、（本小题满分14分）
设
分别为椭圆
的左、右焦点。中学试卷网版权所有 http://www.shijuan.cn
（1）若椭圆
上的点
到两点的距离之和等于4，写出椭圆的方程和焦点坐标；
（2）设点
是（1）中所得椭圆上的动点，求线段
的中点的轨迹方程；
（3）已知椭圆具有性质：若是椭圆上关于原点对称的两个点，点是椭圆上任意一点，当直线
的斜率都存在，并记为
时，那么
之积是与点位置无关的定值。试对双曲线
写出具有类似特性的性质，并加以证明。
2005-2006学年第一学期期末考试题
高二数学科目数学答题卡
（考试时间：90分钟；考试形式：闭卷）
注意事项：本试卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷选择题，请用2B铅笔填涂在机读卡上；第Ⅱ卷为非选择题，请用黑色笔答在答题卡上。
一、选择题：（每题5分,共60分，只有一选项符合题目要求）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 |
二、填空题：（每题4分,共16分）
13
14
15
16
三、解答题：（共74分）
17、（本小题满分12分）
已知，且成等比数列，求证：
18、（本小题满分12分）
已知，则不等式的解集。
19、（本小题满分12分）
已知圆与圆：外切，且两圆的公切线为，已知圆的圆心落在直线上，求圆的方程。
20、（本小题满分12分）
设直线与圆交于两点，且关于直线对称，求不等式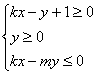表示的平面区域的面积。
21、（本小题满分12分）
已知正三角形ABC的两顶点A,B在轴上，另一顶点在轴上，DE为平行于轴的正ABC的中位线，双曲线M经过D,E两点，且以A,B为焦点，试求此双曲线的离心率的值。
22、（本小题满分14分）
设分别为椭圆
的左右焦点。
（1）若椭圆上的点到两点的距离之和等于4，写出椭圆的方程和焦点坐标；
（2）设点是（1）中所得椭圆上的动点，求线段的中点的轨迹方程；
（3）已知椭圆具有性质：若是椭圆上关于原点对称的两个点，点是椭圆上任意一点，当直线的斜率都存在，并记为时，那么之积是与点位置无关的定值。试对双曲线写出具有类似特性的性质，并加证明。
2005－2006学年下学期期末考试
高二数学科目数学答案
一、选择题：（每题5分,共60分，只有一选项符合题目要求）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | D | D | A | A | C | B | D | A | B | A | A | C |
二、填空题：（每题4分,共16分）
13 4 14
15 
16 ④
三、解答题
17、证明：左-右=
，∵
∴=
得证
18、解：原不等式等价于
∴
19、解：易
，
，圆心坐标
为落在直线上，解得
=-4，所以圆的方程
20、解：因关于直线对称，∴直线垂直于，∴
=1，∴圆心在上，∴
=-1，所以不等式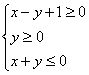
表示的平面区域的面积为
21、解：设
，则的坐标为
，故点E的坐标为
，设双曲线的方程为，双曲线又过点E，所以
，既得
，
所以
，由
，所以
。（或用双曲线的定义解同样给分）
22、（1）椭圆方程为
，焦点坐标为
；（2）线段的中点的轨迹方程
；（3）类似特性的性质：若是双曲线：上关于原点对称的两个点，点是双曲线上任意一点，当直线的斜率都存在，并记为时，那么之积是与点位置无关的定值。
中学试卷网版权所有 http://www.shijuan.cn
设点的坐标为
，点
的坐标为
，其中
，又设点的坐标为
，由
得
，将
，
代入上式得
。