高二级数学2-3检测题
班级 姓名 学号 得分
一、 选择题：（每题6分，共60分）
1.
，则
等于
（
）
A． 
B.
C.
D.
2.如果复数z=3+ai满足条件
，那么实数a的取值范围是（ ）
A.
B.(-2,2)
C.(-1,1)
D.
3.
的值为（
）
A．1
B．
C.
D．2
4.一个质点在直线上运动，其任一时刻t(单位：s)的位置是f(t)=3t-t2 (单位：cm)，则此质点的最大位移和最大速度分别为（ ）
A．1cm,
cm/s B.
C
D．1cm,3cm/s
5.复数
等于（ ）
A.
B .
C. 
D. 
6．由0、1、2、…、9十个数码和一个虚数单位i可以组成虚数的个数为（ ）
A.100 B.10 C.9 D.90
7.函数
，则（ ）
A.f(x)在(0,10)上是增函数 B. f(x)在(0,10)上是减函数
C. f(x)在(0,e)上是增函数，在(e,10)上是减函数
D.f(x)在上(0,e)是减函数，在(e,10)上是增函数
8.利用数学归纳法证明“（n+1）(n+2)(n+3)…(n+n)=2n×1×3×…(2n-1)(n∈N*)”时，从”n=k”变到“n=k+1”时，左边应增添的因式是（ ）
A.2k+1 B.
C.
D.
9.将4个不同的小球放入3个不同的盒子，其中每个盒子都不空的放法有（ ）
A.
种
B.
种
C. 18种
D.36种
10.由直线y=x-4，曲线
以及x轴所围成的图形面积为（ ）
A.
B.13
C.
D.15
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二．填空题：（每题6分
11.曲线
在点
处的切线方程为 .
12.复数z满足
，那么z= 。
13.若集合A={-3，-2，-1，0，1，2}，P(x,y)是平面上的点,x,y∈A,则
（1）P可以表示 个平面上的点； （2）P可以表示 个坐标轴上的点；
（3）P可以表示 个第二象限的点；
（4）P可以表示 个不在直线y=x上的点。
14.观察下列各式：1=0+1
2+3+4=1+8
5+6+7+8+9=8+27
10+11+12+13+14+15+16=27+64
你所做出的猜想是 。
三、 解答题：
15.(15分)已知x,y,z是互不相等的正数，且x+y+z=1。求证：
。
16.（15）分设点P(a,b)对应于复数z，点Q对应于复数2z+3-4i，如果点P在曲线
上移动，求点Q的轨迹方程。
17.（18分）函数
对任意实数
都有
.
（Ⅰ）求
的值；
（Ⅱ）若
，求
的值，猜想
的表达式并用数学归纳法证明你的结论；
（Ⅲ）若
，求证：
18.（18分）已知
函数
的图像与函数
的图象相切.
（Ⅰ）求b与c的关系式（用c表示b）；
（Ⅱ）设函数
，
（ⅰ）当
时，在函数
的图像上是否存在点
，使得在点
的切线斜率为
，若存在，求出点的坐标；若不存在，说明理由.
（ⅱ）若函数在
内有极值点，求c的取值范围。
高二数学2-3测验答案
一.选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | D | C | B | B | D | C | C | D | A |
二.填空题：
11.y=2x 12.2+i 13.(1)36 (2)11 (3)6 (4)30
14.(n2-2n+2)+(n2-2n+3)+…+n2=(n-1)3+n3
三.解答题：
15.证明：
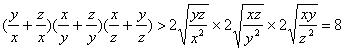
16.解：2z+3-4i=(2a+3)+(2b-4)I ……5’
设Q(x,y),则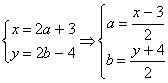
……5’
……5’
17. 解证：（Ⅰ）令
得
……3′
（Ⅱ），
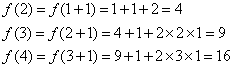………6′
猜想
，下用数学归纳法证明之.
（1）当n=1时,f(1)=1,猜想成立；
（2）假设当n=k时，猜想成立，即 f(k)=k2
则当n=k+1时， f(k+1)=f(k)+f(1)+2k×1=k2+2k+1=(k+1)2
即当n=k+1时猜想成立。
由（1）、（2）可知，对于一切n∈N*猜想均成立。 ………9′
（Ⅲ），则
假设
时命题成立，即
，则
,
由上知，则
.
………18′
18. 解：（Ⅰ）依题意，令
……4′
（Ⅱ）
（ⅰ）当时，
，
，若存在满足条件的点M，则有：
,
,即这样的点M存在，且坐标为
………12′
（ⅱ）
令
(x)=0，即3x2+4bx+b2+c=0；而
=16b2-12(b2+c)=4(b2-3c)，
若=0，则(x)=0有两个相等的实根，设为x0，此时(x)的变化如下：
| x |
| x0 | （ |
|
| + | 0 | + |
于是
不是函数的极值点.
的变化如下：
| x |
| x1 |
|
| （ |
|
| + | 0 | — | 0 | + |
由此，
的极小值点.
综上所述，当且仅当
………18′