![]() 诏安一中05—06学年下学期期中考
诏安一中05—06学年下学期期中考
高二数学(理)试卷
时间:120分钟 满分:150分 命题人:沈顺发 审核人:许维民
一.![]()


 选择题(每小题5分,共60分)
选择题(每小题5分,共60分)
1.空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为( )
A.3 B.1或3 C.1或2 D.2或3
2. 若![]() 为异面直线,直线c∥a,则c与b的位置关系是 ( )
为异面直线,直线c∥a,则c与b的位置关系是 ( )
A.相交 B.异面 C.平行 D. 异面或相交
3.已知![]() ( )
( )
A.150° B.90° C.60° D.30°
4.设向量![]() 是空间一个基底,则一定可以与向量
是空间一个基底,则一定可以与向量![]() 构成空间的另
构成空间的另
一个基底的向量是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下面表述正确的是 ( )
A、空间任意三点确定一个平面 B、分别在不同的三条直线上的三点确定一个平面
C、直线上的两点和直线外的一点确定一个平面 D、不共线的四点确定一个平面
6. 直线![]() 与
与![]() 垂直,
垂直,![]() 又垂直于平面
又垂直于平面![]() ,则
,则![]() 与
与![]() 的位置关系是
( )
的位置关系是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]() 或
或![]()
7.若![]() 表示直线,
表示直线,![]() 表示平面,则下列命题中,正确命题的个数为
( )
表示平面,则下列命题中,正确命题的个数为
( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
A、1个 B、2个 C、3个 D、4个
8.已知空间三点O(0,0, 0), A(-1, 1, 0), B(0, 1, 1), 在直线OA上有一点H满足BH⊥OA,则点H的坐标为 ( )
A.(-2, 2, 0) B.(2, -2, 0) C.![]() D.
D.![]()
9.若![]() 则
则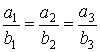 是
是![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
10.在正方体A1B1C1D1—ABCD中,AC与B1D所成的角的大小为 ( )
|
C.![]() D.
D.![]()
|
①过P点可作直线k与a,b都相交;
②过P点可作平面与a,b都平行;
③过P点可作直线与a,b都垂直;
④过P点可作直线k与a,b所成角都等于50![]() .
.
这四个命题中正确命题的序号是 ( )
A.①、②、③ B.②、③、④
C.② D.③、④
12.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点A、B、C一定共面的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二.填空题(每小题5分,共20分)
13.直线![]() ,直线
,直线![]() ,且
,且![]() ,则a与b的位置关系为 。
,则a与b的位置关系为 。
14.
已知![]() =(—4,2,x),
=(—4,2,x),![]() =(2,1,3),且
=(2,1,3),且![]() ⊥
⊥![]() ,则x= 。
,则x= 。
15.在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,则AC1长为_______。
,则AC1长为_______。
16.如图,AO⊥平面α,点O为垂足,BC![]() 平面α,BC⊥OB;
平面α,BC⊥OB;
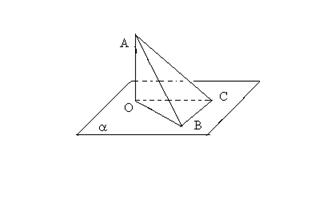 若
若![]()
![]() , 则cos
, 则cos![]() 的值是
。
的值是
。
|
![]()
![]()


 诏安一中05—06学年下学期期中考
诏安一中05—06学年下学期期中考
高二数学(理)试卷
时间:120分钟 满分:150分 命题人:沈顺发 审核人:许维民
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一.选择题(12![]() 5=60)
5=60)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二。填空题(4![]() 5=20)
5=20)
13. ;14. ;15. ;16. 。
三.解答或证明题
|
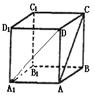
E是DC的中点,取如图所示的空间直角坐标系.
(1)写出A、B1、E、D1的坐标;
(2)求AB1与D1E所成的角的余弦值.
|
18.(10分)已知![]() =CD,EA
=CD,EA![]()
![]() ,垂足为A,EB
,垂足为A,EB![]()
![]() ,垂足为B,求证CD
,垂足为B,求证CD![]() AB。
AB。
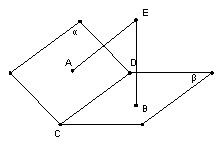
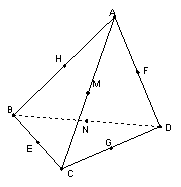
19. (12分)如图,H、 E、F、G、M、N分别是空间四边形ABCD的四边及其对角线AC,BD的中点,若AB=BC=CD=DA=AC=BD,求证![]()
 | ||||
| ||||
| |
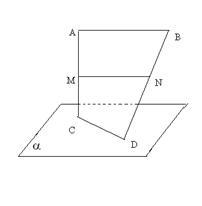 20.(12分)已知AB与CD为异面线段,CD
20.(12分)已知AB与CD为异面线段,CD![]() 平面α,AB//α,M、N分别是线段AC与BD的中点,求证:MN//平面
平面α,AB//α,M、N分别是线段AC与BD的中点,求证:MN//平面![]() 。
。
|
(1)证明 ![]() 平面
平面![]() ;
;
(2)证明![]() 平面EFD;
平面EFD;
![]()
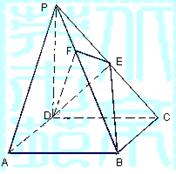
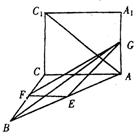
![]() 22. (14分)如图,正方形ACC1A1与等腰直角△ACB中, CC1
22. (14分)如图,正方形ACC1A1与等腰直角△ACB中, CC1![]() BC,∠ACB=90°,
BC,∠ACB=90°,
E、F分别是AB、BC的中点, G是AA1上的点.
(I)若AC1⊥EG,试确定点G的位置;
![]()
![]() (II)在满足条件(1)的情况下,试求cos<AC,GF>的值.
(II)在满足条件(1)的情况下,试求cos<AC,GF>的值.
![]()
![]()
诏安一中05—06学年高二下学期期中考数学试卷
参考答案:
一.选择题(12![]() 5=60)
5=60)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | A | C | C | D | C | C | A | D | D | D |
三.填空题(4![]() 5=20)
5=20)
13.平行或异面 14. 2 15. ![]() 16.
16.![]()
三、解答题
![]()
![]() 17.①A(2,2,0),B1(2,0,2),E(0,1,0),D1(0,2,2)
17.①A(2,2,0),B1(2,0,2),E(0,1,0),D1(0,2,2)
②AB1=(0,-2,2),D1E=(0,-1,-2)
![]()
![]() COS< AB1, D1E>=
COS< AB1, D1E>=![]()
故
AB1 与D1E所成的角的余弦值为![]()
18. ∵![]() =CD,∴ CD
=CD,∴ CD![]()
![]()
∵EA![]()
![]() ∴ CD
∴ CD![]() EA
EA
同理: CD![]() EB
EB
∴CD![]() 平面EAB
平面EAB
∴CD![]() AB
AB
19.解:


20.连结AD,取AD中点E
∵N是BD的中点
∴![]()
又![]()
∴![]()
∵M是AC的中点
∴![]()
∴![]()
∴平面MEN∥平面![]()
∴MN∥平面![]()
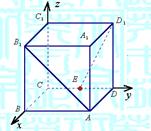
21.解:如图所示建立空间直角坐标系,D为坐标原点.设![]()
(1)证明:连结AC,AC交BD于G.连结EG.
依题意得![]()
![]() 底面ABCD是正方形,
底面ABCD是正方形, ![]() 是此正方形的中心,
是此正方形的中心,
故点G的坐标为![]() 且
且![]()
![]() . 这表明
. 这表明![]() .
.
而![]() 平面EDB且
平面EDB且![]() 平面EDB,
平面EDB,![]() 平面EDB。
平面EDB。
(2)证明:依题意得![]() 。又
。又![]() 故
故![]()
![]() , 由已知
, 由已知![]() ,且
,且![]() 所以
所以![]() 平面EFD.
平面EFD.
22.解:(Ⅰ)由正方形ACC1A1与等腰直角△ACB互相
垂直,∠ACB=90°,∴BC⊥AC,∴BC⊥CC1.以C为坐标原点,建立空间直角坐标
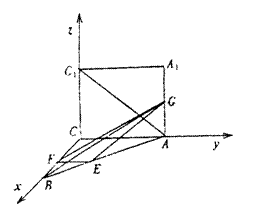 系C—xyz,如图.(2分)
系C—xyz,如图.(2分)
设AC=CB=a,AG=x,则A(0,a,0).
C1(0,0,a),G(0,a,x),E(-![]() ,
,![]() ,0).
,0).
![]()
![]() AC1=(0,-a,a),EG=(-
AC1=(0,-a,a),EG=(-![]() ,
,![]() ,x).
,x).
![]()
![]() ∵AC1·EG=0,∴-
∵AC1·EG=0,∴-![]() +xa=0.
+xa=0.
∴x=![]() ,∴G为AA1的中点.
,∴G为AA1的中点.
(Ⅱ)∵G(0,a,![]() ),F(
),F(![]() ,0,0),
,0,0),
![]()
![]()
![]()
![]() ∴GF=(
∴GF=(![]() ,-a,-
,-a,-![]() ),AC1=(0,-a,a).
),AC1=(0,-a,a). ![]()
![]()
![]()
![]() ∴ GF =
∴ GF =![]() a, AC1 =
a, AC1 =![]() a,∴GF·AC1=a2-
a,∴GF·AC1=a2-![]() =
=![]() .∴cos<AC1,GF>=
.∴cos<AC1,GF>=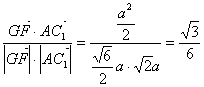 .
.